OPTIMIZATION IN FUNCTION SPACES
AMOL SASANE
DEPARTMENT OF MATHEMATICS LONDON SCHOOL OF ECONOMICS
DOVER PUBLICATIONS, INC. MINEOLA, NEW YORK
Copyright Copyright 2016 by Amol Sasane
All rights reserved.
Bibliographical NoteOptimization in Function Spaces is a new work, first published by Dover Publications, Inc., in 2016, as part of the Aurora: Dover Modern Math Originals series.
International Standard Book NumbereISBN-13: 978-0-486-81096-6 Manufactured in the United States by RR Donnelley 789454012016 www.doverpublications.com
Contents
Introduction
The subject matter of this book is

It is thus natural to begin by explaining what we mean by this. If we ignore the in function spaces part, we see that the subject matter is a part of optimization. In optimization, we know that the basic object of study is a real-valued function
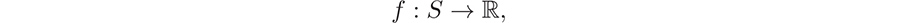
defined on a set
S, and the central problem is that of maximizing or minimizing
f:
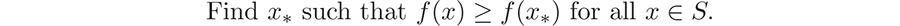
This is the case of minimizing
f.
In maximization problems, the inequality above is reversed. There is no real difference between maximization and minimization problems: indeed, if we learn to solve minimization problems, we also know how to solve maximization problems, because we can just look at f instead of f. Let f : S be a given function on a set S, and define f : S
be a given function on a set S, and define f : S by
by 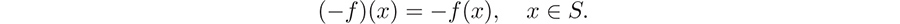 Show that x*S is a maximizer for f if and only if x* is a minimizer for f. Why bother with optimization problems? In applications, we are often faced with choices or options, that is, different ways of doing the same thing. Imagine, for example, traveling to a certain place by rail, bus or air. Given the choice, it makes sense that we then choose the best possible option.
Show that x*S is a maximizer for f if and only if x* is a minimizer for f. Why bother with optimization problems? In applications, we are often faced with choices or options, that is, different ways of doing the same thing. Imagine, for example, traveling to a certain place by rail, bus or air. Given the choice, it makes sense that we then choose the best possible option.
For example, one might wish to seek the cheapest means of transport. The set S in our optimization problem is thus the set of possible choices. To each choice xS, we assign a number f(x) 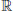 (measuring how good that choice is), and this gives the cost function f : S
(measuring how good that choice is), and this gives the cost function f : S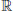 to be minimized. In an optimization problem of minimizing f : S
to be minimized. In an optimization problem of minimizing f : S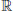 , the set S is called the feasible set, and the function f is called the objective function. Thus, in optimization, one studies the problem
, the set S is called the feasible set, and the function f is called the objective function. Thus, in optimization, one studies the problem 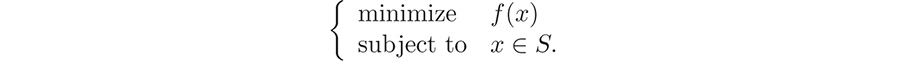 Depending on the nature of S and f, the broad subject of optimization is divided into subdisciplines such as
Depending on the nature of S and f, the broad subject of optimization is divided into subdisciplines such as  and so on. In this book, we will study dynamic optimization in continuous-time. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years.
and so on. In this book, we will study dynamic optimization in continuous-time. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years.
Suppose that x(t) denotes the total amount of copper removed up to time t [0, T]. Since the operation is over a large time period, we may assume that this x is a function living on the continuous-time interval [0, T]. The company has the freedom to choose its mining operation: x can be any nondecreasing function on [0, T] such that x(0) = 0 (no copper removed initially) and x(T) = Q (all copper removed at the end of the mining operations). 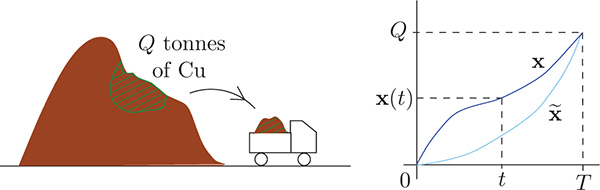 Figure 1. Several possible mining operations: x,
Figure 1. Several possible mining operations: x,  , . The cost of extracting copper per unit tonne at time t is given by
, . The cost of extracting copper per unit tonne at time t is given by 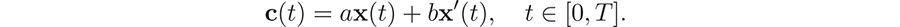 Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the left over copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example, due to machine replacement costs).
Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the left over copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example, due to machine replacement costs).
We dont need to follow the exact reasoning behind this formula; this is just a model that the optimizer has been given. If the company decides on a particular mining operation, say x : [0, T]  , then the overall cost f(x)
, then the overall cost f(x)  over the whole mining period [0, T] is given by
over the whole mining period [0, T] is given by 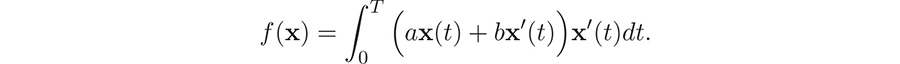 Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f (x) given above. Hence, the mining company is faced with the following natural problem: Which mining operation x incurs the least cost? In other words,
Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f (x) given above. Hence, the mining company is faced with the following natural problem: Which mining operation x incurs the least cost? In other words, 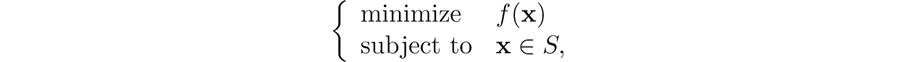 where S denotes the set of all (continuously differentiable) functions x : [0, T]
where S denotes the set of all (continuously differentiable) functions x : [0, T] 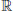 such that x(0) = 0 and x
such that x(0) = 0 and x












 It is thus natural to begin by explaining what we mean by this. If we ignore the in function spaces part, we see that the subject matter is a part of optimization. In optimization, we know that the basic object of study is a real-valued function
It is thus natural to begin by explaining what we mean by this. If we ignore the in function spaces part, we see that the subject matter is a part of optimization. In optimization, we know that the basic object of study is a real-valued function 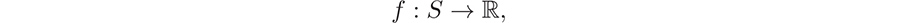 defined on a set S, and the central problem is that of maximizing or minimizing f:
defined on a set S, and the central problem is that of maximizing or minimizing f: 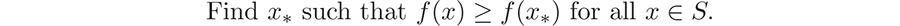 This is the case of minimizing f.
This is the case of minimizing f. 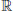 be a given function on a set S, and define f : S
be a given function on a set S, and define f : S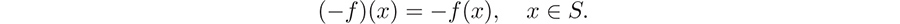 Show that x*S is a maximizer for f if and only if x* is a minimizer for f. Why bother with optimization problems? In applications, we are often faced with choices or options, that is, different ways of doing the same thing. Imagine, for example, traveling to a certain place by rail, bus or air. Given the choice, it makes sense that we then choose the best possible option.
Show that x*S is a maximizer for f if and only if x* is a minimizer for f. Why bother with optimization problems? In applications, we are often faced with choices or options, that is, different ways of doing the same thing. Imagine, for example, traveling to a certain place by rail, bus or air. Given the choice, it makes sense that we then choose the best possible option.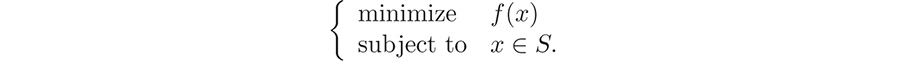 Depending on the nature of S and f, the broad subject of optimization is divided into subdisciplines such as
Depending on the nature of S and f, the broad subject of optimization is divided into subdisciplines such as  and so on. In this book, we will study dynamic optimization in continuous-time. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years.
and so on. In this book, we will study dynamic optimization in continuous-time. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years. Example 0.2. Imagine a copper mining company that is mining in a mountain, which has an estimated amount of Q tonnes of copper, over a period of T years. Figure 1. Several possible mining operations: x,
Figure 1. Several possible mining operations: x,  , . The cost of extracting copper per unit tonne at time t is given by
, . The cost of extracting copper per unit tonne at time t is given by 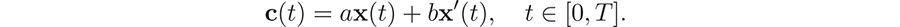 Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the left over copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example, due to machine replacement costs).
Here a, b are given positive constants. The expression is reasonable, since the term ax(t) accounts for the fact that when more and more copper is taken out, it becomes more and more difficult to find the left over copper, while the term bx(t) accounts for the fact that if the rate of removal of copper is high, then the costs increase (for example, due to machine replacement costs).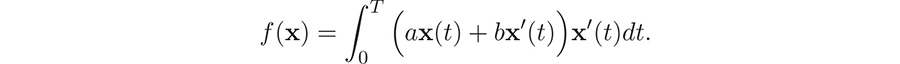 Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f (x) given above. Hence, the mining company is faced with the following natural problem: Which mining operation x incurs the least cost? In other words,
Indeed, x(t)dt is the incremental amount of copper removed at time t, and if we multiply this by c(t), we get the incremental cost at time t. The total cost should be the sum of all these incremental costs over the interval [0, T], and so we obtain the integral expression for f (x) given above. Hence, the mining company is faced with the following natural problem: Which mining operation x incurs the least cost? In other words, 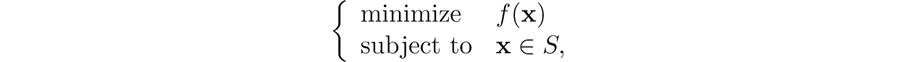 where S denotes the set of all (continuously differentiable) functions x : [0, T]
where S denotes the set of all (continuously differentiable) functions x : [0, T]