GENERALIZED FUNCTIONS AND PARTIAL DIFFERENTIAL EQUATIONS AVNER FRIEDMAN The Ohio State University DOVER PUBLICATIONS, INC. Mineola, New York Copyright Copyright 1963 by Avner Friedman All rights reserved. Bibliographical Note This Dover edition, first published in 2005, is an unabridged republication of the work originally published by Prentice-Hall, Inc., Englewood Cliffs, New Jersey, in 1963. Library of Congress Cataloging-in-Publication Data Friedman, Avner. Generalized functions and partial differential equations / Avner Friedman.
p. cm.
Originally published: Englewood Cliffs, N.J. : Prentice-Hall, 1963. Includes bibliographical references and indexes. eISBN 13: 978-0-486-15291-2 1. Differential equations, Partial. 2.
Theory of distributions (Functional analysis) I. Title. QA377.F74 2005
515.353dc22 2005051302 Manufactured in the United States of America
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501 To My Parents PREFACE In recent years important progress has been made in the theory of partial differential equations due, to a large extent, to the development of new methods. The purpose of this book is to give a self-contained account of one of the main directions of this recent progress. The theory of generalized functions and, in particular, the theory of distributions, will be developed in detail.
This theory will then be applied to solve a variety of problems in partial differential equations. The use of generalized functions (and of distributions) in solving these problems is not merely a matter of convenience. In fact, the need to use generalized functions arises in a natural way, and an attempt to avoid them will result in far more complicated proofs and in less decisive theorems. The theory of generalized functions has been successfully applied also in other fields of mathematics, e.g., representation of locally compact groups, exterior differential forms, operational calculus, probability, etc. Beside the topics in differential equations covered in this book, generalized functions occur also in questions of eigenvalue expansions, approximation theorems, division problems, etc. The theory of distributions was developed by L.
Schwartz in 194548. A detailed exposition appears in his books [54]. The introduction of generalized functions of any class and their use in solving the Cauchy problem were given by Gelfand and Shilov in 1953. In 195658 they published three volumes (in Russian) on the subject [2426]. A large part of the present book is based upon material from the books of Schwartz and of Gelfand and Shilov. In addition, the book contains more recent applications to differential equations as well as a more complete treatment (than that of Gelfand and Shilov) of the Cauchy problem.
The reader is assumed to have a sound knowledge of both real variables and complex variables. Familiarity with the basic theory of functional analysis (in particular, normed spaces) is desirable but not necessary. We briefly describe the contents of the book. we characterize the polynomials P(x) such that all the solutions of P(/x)u = 0 are infinitely differentiable functions, and also solve, in the whole space, the equation P(/x)u = f(x). At the end of each chapter some easy problems are given with the purpose of familiarizing the reader with the material. Bibliographical remarks and bibliography will be found at the end of the book.
It is a pleasure to express my gratitude to my wife, for doing an excellent job of typing the manuscript. While working on the book I was partially supported by ONR contracts and by the Alfred P. Sloan Foundation. Avner Friedman CONTENTS CHAPTER 1 LINEAR TOPOLOGICAL SPACES In this chapter we give the functional analysis background that will be needed in this book. In addition to a brief summary of some fundamental concepts and theorems from the theory of linear topological spaces and of normed spaces, we introduce the concepts of countably normed spaces and of perfect spaces and prove in detail some basic results concerning these spaces and their conjugate spaces. 1. 1.
Topological Spaces and Metric Spaces Let X be a set of points and let T be a system of subsets of X having the following properties: 1. the empty set and the set X belong to T, 2. the union of any number of sets of T belongs to T, and 3. the intersection of any finite number of sets of T belongs to T. We then say that T defines a topology on X and we call the pair (X, T) a topological space. When there is no confusion we designate (X, T) by X.
The sets of T are called open sets. If T1 and T2 define two topologies on X, we say that the topology defined by T1 is weaker (or coarser) than the topology defined by T2 or, equivalently, that the topology defined by T2 is stronger (or finer) than the topology defined by T1 if every set of T1 contains a set of T2. If the T1 topology is both weaker and stronger than the T2 topology, then we say that the topologies are equivalent. A system of open sets is said to constitute a basis of a topology if every open set is the union of sets of the system. A neighborhood of a point x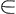 X (of a set AX) is any set of X which contains an open set containing x (including A). A system W of neighborhoods of a point x is called a basis of neighborhoods (or a neighborhood basis) at x if every neighborhood of x contains some set of W.
X (of a set AX) is any set of X which contains an open set containing x (including A). A system W of neighborhoods of a point x is called a basis of neighborhoods (or a neighborhood basis) at x if every neighborhood of x contains some set of W.
Two neighborhood bases at the same point x are said to be equivalent if each neighborhood of either one of them contains a neighborhood of the other. A similar definition holds for bases of a topology. Taking a neighborhood basis at each point of X, the set whose elements are all the neighborhoods thus obtained is clearly a basis of the topology. X is said to satisfy the first countability axiom if there exists a countable neighborhood basis at each point of X. X is said to satisfy the second countability axiom if there exists a countable basis for X. x is an interior point of a set M if there exists a neighborhood of x contained in M. x is an interior point of a set M if there exists a neighborhood of x contained in M.
The set of all interior points of M is called the interior of M and is denoted int M. Int M is an open set, and M is open if and only if M = int M. x is a limit point of M if for every neighborhood V of x, Vx intersects M, i.e., (Vx) M 0. The closure of M (denoted by 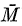 ) is the union of M and the set of all limit points of M.
) is the union of M and the set of all limit points of M. 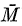 is a closed set and M is closed if and only if
is a closed set and M is closed if and only if 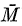 = M.
= M. 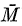 int M is called the boundary of M.
int M is called the boundary of M.
A sequence {xn} is said to be convergent to x (we write xn
Next page













 X (of a set AX) is any set of X which contains an open set containing x (including A). A system W of neighborhoods of a point x is called a basis of neighborhoods (or a neighborhood basis) at x if every neighborhood of x contains some set of W.
X (of a set AX) is any set of X which contains an open set containing x (including A). A system W of neighborhoods of a point x is called a basis of neighborhoods (or a neighborhood basis) at x if every neighborhood of x contains some set of W.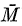 ) is the union of M and the set of all limit points of M.
) is the union of M and the set of all limit points of M.