Marcelo Epstein - Partial Differential Equations: Mathematical Techniques for Engineers
Here you can read online Marcelo Epstein - Partial Differential Equations: Mathematical Techniques for Engineers full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: Springer, genre: Computer. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Partial Differential Equations: Mathematical Techniques for Engineers
- Author:
- Publisher:Springer
- Genre:
- Year:2017
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Partial Differential Equations: Mathematical Techniques for Engineers: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Partial Differential Equations: Mathematical Techniques for Engineers" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Marcelo Epstein: author's other books
Who wrote Partial Differential Equations: Mathematical Techniques for Engineers? Find out the surname, the name of the author of the book and a list of all author's works by series.













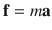 , we observe a clear transition from merely descriptive laws, that apply to a small number of phenomena, to structural and explanatory laws encompassing almost universal situations, as suggested in Fig.. This feat was achieved by Newton, and later perfected by others, in formulating general physical laws in the small (differentials) and obtaining the description of any particular global phenomenon by means of a process of integration (quadrature).
, we observe a clear transition from merely descriptive laws, that apply to a small number of phenomena, to structural and explanatory laws encompassing almost universal situations, as suggested in Fig.. This feat was achieved by Newton, and later perfected by others, in formulating general physical laws in the small (differentials) and obtaining the description of any particular global phenomenon by means of a process of integration (quadrature). 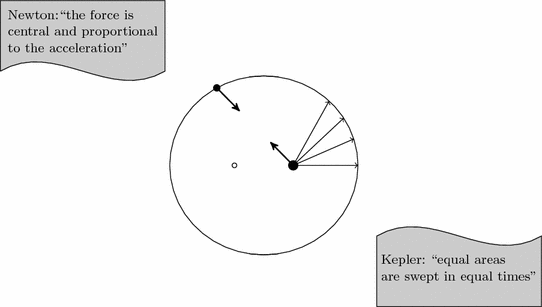
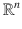
 the set of real numbers. Recall the notion of Cartesian product of two sets, A and B , namely, the set
the set of real numbers. Recall the notion of Cartesian product of two sets, A and B , namely, the set 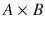 consisting of all ordered pairs of the form ( a , b ), where a belongs to A and b belongs to B . More formally,
consisting of all ordered pairs of the form ( a , b ), where a belongs to A and b belongs to B . More formally, 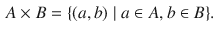
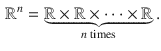
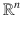 can be viewed as the set of all ordered n -tuples of real numbers. It has a natural structure of an n -dimensional vector space (by defining the vector sum and the multiplication by a scalar in the natural way).).
can be viewed as the set of all ordered n -tuples of real numbers. It has a natural structure of an n -dimensional vector space (by defining the vector sum and the multiplication by a scalar in the natural way).). 
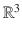
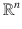 has to be seen as carrying its own copy of
has to be seen as carrying its own copy of 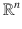 , containing all the vectors issuing from that point. This is an important detail. For example, consider the surface of a sphere. This is clearly a 2-dimensional entity. By means of lines of latitude and longitude, we can identify a portion of this entity with
, containing all the vectors issuing from that point. This is an important detail. For example, consider the surface of a sphere. This is clearly a 2-dimensional entity. By means of lines of latitude and longitude, we can identify a portion of this entity with 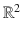 , as we do in geography when drawing a map (or, more technically, a chart ) of a country or a continent. But the vectors tangent to the sphere at a point p , do not really belong to the sphere. They belong, however, to a copy of the entire
, as we do in geography when drawing a map (or, more technically, a chart ) of a country or a continent. But the vectors tangent to the sphere at a point p , do not really belong to the sphere. They belong, however, to a copy of the entire 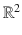 (the tangent plane to the sphere at that point). In the case in which the sphere is replaced by a plane, matters get simplified (and, at the same time, confused).
(the tangent plane to the sphere at that point). In the case in which the sphere is replaced by a plane, matters get simplified (and, at the same time, confused). 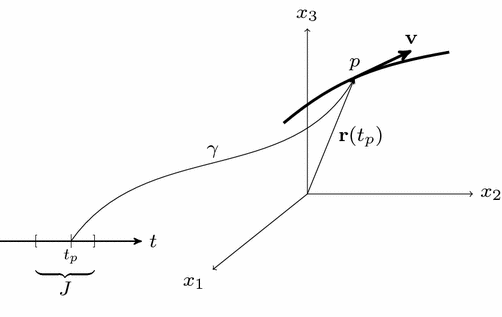
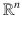
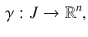
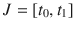 (with
(with 