Avner Friedman The Ohio State University DOVER PUBLICATIONS, INC.
Copyright 1971, 1999 by Avner Friedman All rights reserved.
This Dover edition, first published in 2007, is an unabridged republication of the work published by Holt, Rinehart and Winston, Inc., New York, in 1971.
Dover Publications, Inc., 31 East 2nd Street, Mineola, N.Y. 11501
This book is intended for students who have already completed a one year course in elementary calculus. These students are familiar with the powerful methods of calculus in solving a variety of problems arising in physics, engineering, and geometry. They are therefore sufficiently motivated towards a rigorous treatment of the subject.
Many of the ideas of advanced calculus are by no means simple or intuitive. (It took mathematicians two hundred years to develop them!) Furthermore, for most students this is the first substantial course in mathematics taught in a rigorous way. We have therefore attempted to keep this book on a comfortable level. For example, it has been our experience that the student does not feel at ease with calculus in two or more dimensions. We have therefore deferred the introduction of functions of several variables as long as possible. We feel that further clarity and simplicity is added by avoiding mixture of heuristic and rigorous arguments.
The book contains material for more than a years course; some choice is thus offered. Our own inclination is to omit parts of several sections throughout ; the sections in this chapter are independent of each other. When we refer to a particular section, say to . I would like to thank Andrew J. Callegari and Joseph E. A.F. Tel Aviv, IsraelMay 1971
1. Tel Aviv, IsraelMay 1971part one
FUNCTIONS OF ONE VARIABLE
NUMBERS AND SEQUENCES
The positive integers 1,2, 3, are called
natural numbers. Since we intend to do things rigorously, we cannot be satisfied with our everyday familiarity with these numbers, and we should try to axiomatize their properties. Let us first write down five statements concerning the natural numbers that we feel should be true: (I) 1 is a natural number. (II) To every natural number
n there is associated in a unique way another natural number
n called the
successor of
n. (III) 1 is not a successor of any natural number. (V) Let
M be a subset of the natural numbers such that: (i) 1 is in
M, and (ii) if a natural number is in
M, then its successor also is in
M. (V) Let
M be a subset of the natural numbers such that: (i) 1 is in
M, and (ii) if a natural number is in
M, then its successor also is in
M.
Then M coincides with the set of all the natural numbers. From now on we consider the statements (I)(V) to be axioms. They are called the Peano axioms. The natural numbers will be the objects occurring in the Peano axioms. Axiom (V) is called the principle of mathematical induction. We denote the successor of 1 by 2, the successor of 2 by 3, and so on.
Note that 2 1. Indeed, if 2 = 1, then 1 is the successor of 1, thus contradicting (III). Note next that 3 2. Indeed, if 3 = 2 then, by (IV), 2 = 1, which is false. In general, one can show that all the numbers obtained by taking the successors of 1 any number of times are all different. The proof of this statement, which we shall not give here, is based on induction, that is, on Axiom (V).
We would like to state Axiom (V) in a form more suitable for application: (V) Let P(n) be a property regarding the natural number n, for any n. Suppose that (i) P(1) is true, and (ii) if P(n) is true, P(n) also is true. Then P(n) is true for all n. If we define M to be the set of all natural numbers for which P(n) is true, then (V) follows from (V). If, on the other hand, we define P(n) to be the property that n belongs to M, then (V) follows from (V). Thus (V) and (V) are equivalent axioms.
The Peano axioms give us objects with which to work. We now proceed to define operations on these objects. There are two operations that we consider: addition (+) and multiplication (). To any given pair of natural numbers each of these operations corresponds another natural number. The precise definition of this correspondence is given in the following theorem. There exist unique operations + and . with the following properties: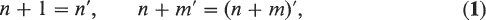
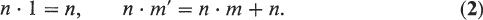 The proof will not be given here. with the following properties:
The proof will not be given here. with the following properties: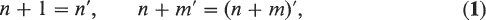
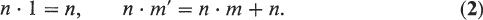 The proof will not be given here.
The proof will not be given here.
We shall often write mn instead of m n. THEOREM 2. The following properties are true for all natural numbers m, n, k: 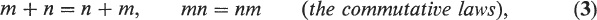
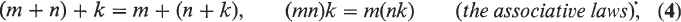
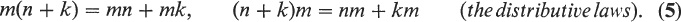 The proof of . We state, without proof, another theorem, known as the trichotomy law: THEOREM 3. Given any natural numbers m and n, one and only one of the following possibilities occurs: (i) m = n. (iii) n = m + y for some natural number y. (iii) n = m + y for some natural number y.
The proof of . We state, without proof, another theorem, known as the trichotomy law: THEOREM 3. Given any natural numbers m and n, one and only one of the following possibilities occurs: (i) m = n. (iii) n = m + y for some natural number y. (iii) n = m + y for some natural number y.
If (ii) holds, we write m > n or n < m, and we say that m is larger or greater than n and that n is smaller or less than m. If either (i) or (ii) holds, we write m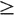 n or n
n or n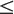 m, and say that m is larger or equal to n and that n is less than or equal to m.
m, and say that m is larger or equal to n and that n is less than or equal to m.
PROBLEMS
1. If
n >
m, then
n +
k >
m +
k. 2. 3. 3.
If n + k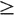 m
m











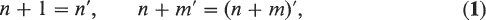
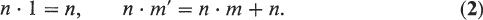 The proof will not be given here. with the following properties:
The proof will not be given here. with the following properties: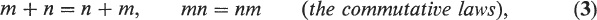
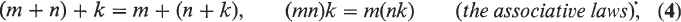
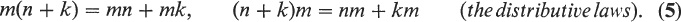 The proof of . We state, without proof, another theorem, known as the trichotomy law: THEOREM 3. Given any natural numbers m and n, one and only one of the following possibilities occurs: (i) m = n. (iii) n = m + y for some natural number y. (iii) n = m + y for some natural number y.
The proof of . We state, without proof, another theorem, known as the trichotomy law: THEOREM 3. Given any natural numbers m and n, one and only one of the following possibilities occurs: (i) m = n. (iii) n = m + y for some natural number y. (iii) n = m + y for some natural number y.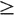 n or n
n or n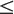 m, and say that m is larger or equal to n and that n is less than or equal to m.
m, and say that m is larger or equal to n and that n is less than or equal to m.