About the Author
Stan Gibilisco is an electronics engineer, researcher, and mathematician. He is the author of
Algebra Know-It-ALL, a number of titles for McGraw-Hill's
Demystified series, more than 30 other technical books and dozens of magazine articles. His work has been published in several languages.
Acknowledgment
I extend thanks to my nephew Tony Boutelle. He spent many hours helping me proofread the manuscript, and he offered insights and suggestions from the viewpoint of the intended audience.
Calculus
Know-It-ALLAPPENDIX A
Worked-Out Solutions to Exercises:
These solutions do not necessarily represent the only way a problem can be figured out.
If you think you can solve a problem faster or better than the way it's done here, by all means try it! Always check your work to be sure your "alternative" answer is correct.
Chapter 1
1. This relation is a function. The domain is the set of all integers, and the range is the set of all nonnegative integers. Every element of the domain maps into one, but only one, element of the range. } This is also a function. } This is also a function.
The domain is the set of all nonnegative integers, and the range is the set of all integers. Every element of the domain maps into one, but only one, element of the range. 2. This relation is a function. Once again, the domain is the set of all integers, and the range is the set of all nonnegative integers. Every element in the domain maps into one, but only one, element of the range.
The inverse, which we get by reversing each ordered pair in the original relation, is {(0,0), (1,1), (1,1), (2,2), (2,2), (3,3), (3,3), (4,4), (4,4),... } This is not a function! The domain is the set of all nonnegative integers, and the range is the set of all integers. With the exception of (0,0), every element of the domain maps into two elements of the range. A function isn't allowed to do that. 3. Let's substitute a letter variable for f(x).
If we use y, the function is written y = 4x 5 To find the inverse, we must solve for x in terms of y. First, we add 5 to each side of the above equation, getting y + 5 = 4x Dividing through by 4 and transposing the sides of the equation left-to-right, we get x = (y + 5)/4 which can be rewritten as x = y/4 + 5/4 This means that f1 (y) = y/4 + 5/4 This is the inverse we seek. It's a linear function of y. 4. This constant function, g(x), has the value 7 regardless of the value of x. If we graph this function and call the dependent variable y, we get a horizontal line through the point y = 7.
The graph of the inverse relation is a vertical line, which fails the vertical-line test, so we know that this inverse is not a function. 5. The equation of the unit circle can be manipulated to get y in terms of x. Here is the original equation for reference: x2 + y2 = 1 If we subtract x2 from each side, we get y2 = 1 x2 Taking the positive-or-negative square root of each side gives us y = (1 x2)1/2 This is a relation whose domain is the set of real numbers between, and including, 1 and 1. The range is also the set of reals between, and including, 1 and 1. The relation is not a function.
With the exception of x = 1 and x = 1, every element of the domain maps into two elements in the range. This fact can be seen by looking at a graph of the unit circle (). The graph fails the vertical-line test as shown by the dashed line, which intersects the circle twice. 6. The equation of the unit circle can be manipulated to get x in terms of y. Once again, here's the original equation for reference: x2 + y2 = 1 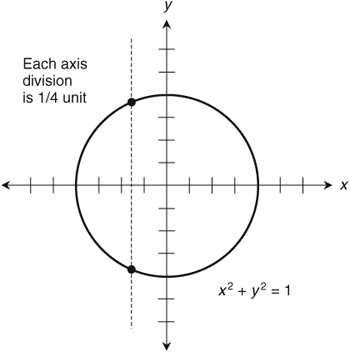 .
.
If we subtract y2 from each side, we get x2 = 1 y2 Taking the positive-or-negative square root of each side gives us x = (1 y2)1/2 This is the same situation as we encountered in the solution to Prob. 5. The names of the variables have been changed, that's all! We have, once again, a relation whose domain and range are both the set of real numbers between, and including, 1 and 1. As before, we don't have a function here because, with the exception of y = 1 and y = 1, every element of the domain maps into two elements in the range. 7. The complete graph of the inverse relation, g1, is a parabola that opens directly toward the right.
If we restrict the range of this relation to the set of positive real numbers, we cut off the lower half of the parabola along with the point (0,0). This leaves only the upper half of the curve, which passes the vertical-line test as shown in . Therefore, g1 becomes a function when the range is restricted to the set of positive reals. It remains a function if we allow the range to include 0 as well as all the positive reals, because the graph still passes the vertical-line test. But we can't extend the range into the negative reals unless we remove at least some of the positive reals. 7 in 8. 7 in 8.
If we restrict the range of g1 to the set of negative reals, we cut off the upper half of the parabola along with (0,0). This leaves only the lower half, which passes the vertical-line test as shown in . Therefore, g1 becomes a function when the range is restricted to the set of negative reals. It remains a function if we also allow the range to include 0, but we can't extend the range into the positive reals unless we remove at least some of the negative reals. 9. If we fill in the gap in the domain for the relation shown in by setting y = 0 when x = 0, we are, in effect, saying that 1/0 = 0, because the relation is y = 1/x The mathematical truth of this can be debated! But it provides us with a y-value for every possible real number x.
The resulting relation is a function, because the graph passes the vertical-line test. The same thing happens with the relation y = tan x graphed in . If we set y = 0 whenever x is an odd-integer multiple of /2, we still have a function of x, because the graph still passes the vertical-line test. We should expect to see some raised eyebrows, however, if we claim that the tangent of /2 is actually equal to 0! 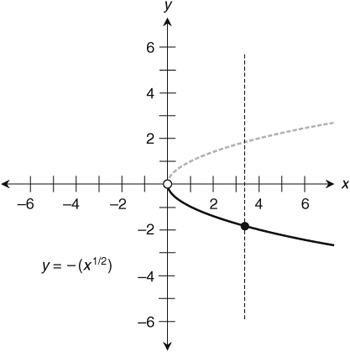 . 10. The inverse of the function shown in is also a function.
. 10. The inverse of the function shown in is also a function.
We can see that this is true by doing the horizontal-line test on the graph. We can take y = 1/x and multiply through by x provided that x 0, getting xy = 1 Then we can divide through by y, again with the constraint that y 0, getting x = 1/y
Chapter 2
1. This sequence starts out at 1/10, and then each succeeding number gets smaller by a factor of 10. The numbers get closer and closer to 0, but never actually reach 0. Therefore, the limit of the sequence is 0. We can write this as
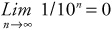
2.
In decimal form, 1/10 = 0.1, 1/102 = 0.01, 1/103 = 0.001, and so on. Let's write the numbers in decimal form and then arrange the sum in as an accountant would do, with each term underneath its predecessor: 













 .
. . 10. The inverse of the function shown in is also a function.
. 10. The inverse of the function shown in is also a function.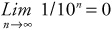 2.
2. 