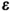RULES OF INTEGRATION

TABLE OF INTEGRALS (The constant of integration is left out.)

ELEMENTARY ALGEBRA OF THE REAL NUMBERS

ALGEBRA OF HYPERREAL NUMBERS Notation:
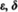
are positive infinitesimals b, c are positive and finite but not infinitesimal H, K are positive infinite. The following are infinitesimal:
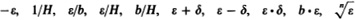
The following are finite but not infinitesimal:
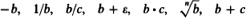
b c is finite (possibly infinitesimal). The following are infinite:
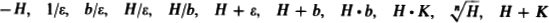
The following can be infinitesimal, finite but not infinitesimal, or infinite:
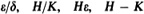
Elementary
Calculus An Infinitesimal Approach Copyright Copyright 1976, 1986, 2012 by H. Jerome Keisler All rights reserved. Bibliographical Note This Dover edition, first published in 2012, is the first publication in book form of the Third Edition of the work originally published in 1976 by Prindle, Weber, and Schmidt, Boston. Jerome. Jerome.
Elementary calculus : an infinitesimal approach / H. Jerome Keisler. 3rd ed. p. cm. This Dover edition, first published in 2012, is the first publication in book form of the Third Edition of the work originally published in 1976 by Prindle, Weber, and Schmidt, Boston.
Includes index. ISBN-13: 978-0-486-48452-5 ISBN-10: 0-486-48452-1 1. Calculus. I. Title. QA303.2K44 2012 515dc23 2011033656 Manufactured in the United States by Courier Corporation
48452101
www.doverpublications.com Dedicated to my sons, Randall, Jeffrey, and Thomas
PREFACE TO THE
THIRD EDITION
This book contains all the usual topics in an elementary calculus course, plus one extra concept that makes the basic ideas more easily understood by beginning students.
This concept is the infinitesimal, or infinitely small number. The calculus was originally developed in the 1670s by Leibniz and Newton using infinitesimals in an informal way, and infinitesimals were given a rigorous foundation by Abraham Robinson in 1960. The work is designed as the main textbook for a three or four semester calculus course. It has been used at both the college and high school levels. Because of its unique approach with infinitesimals, it can also serve as a supplementary book for courses based on other textbooks, and as an interesting refresher for those who have had calculus courses in the past. In addition, it can be a starting point for mathematicians, scientists, and engineers who want to learn about the recent use of infinitesimals beyond calculus.
The First Edition of this book was published in 1976, and a considerably revised Second Edition was published in 1986, both by Prindle, Weber, and Schmidt. When the Second Edition went out of print in 1992, the copyright was returned to me as the author. Since 2002, the Second Edition with minor revisions has been available free in digital form under a Creative Commons License. It can be downloaded at http://www..math.wisc.edu/~keisler/calc. It is listed by the California Digital Textbook Initiative as meeting all content standards for calculus. Many people find it easier and more convenient to learn mathematics from a printed book.
With this Third Edition, Dover Publications has given people the option of purchasing a high-quality affordable printed version of the free digital book. I have written a higher-level companion to this book, Foundations of Infinitesimal Calculus (2007). This companion is intended for instructors and advanced students. It is a self-contained treatment of the mathematical background for this book, and can be a bridge to more advanced topics. It is freely available online at http://www.Math.wisc.edu/~keisler/foundations. Since 1960, modern infinitesimals have been applied to many areas of mathematics, as well as to the physical sciences and economics.
For the most part, these applications have been reported in professional journal articles and in proceedings of conferences, but I will mention two books on the subject. Nonstandard Methods in Stochastic Analysis and Mathematical Physics , by Sergio Albeverio, et. al., is currently available from Dover Publications. The forthcoming book Infinitesimal Methods in Mathematical Economics by Robert M. Anderson is available online at http://www.econ.berkeley.edu/~anderson/Book.pdf. H.
Jerome Keisler June, 2011
PREFACE TO THE
SECOND EDITION
In this second edition, many changes have been made based on nine years of classroom experience. There are major revisions to the first six chapters and the Epilogue, and there is one completely new chapter, on vector calculus. begins with new material on finding a volume by integrating areas of cross sections. Only minor changes and corrections have been made to , infinitesimals are used to give a simple proof that every differential equation y = f ( t, y ), where f is continuous, has a solution. The proof of this fact is beyond the scope of a traditional elementary calculus course, but is within reach with infinitesimals. H. H.
Jerome Keisler
PREFACE TO THE
FIRST EDITION
The calculus was originally developed using the intuitive concept of an infinitesimal, or an infinitely small number. But for the past one hundred years infinitesimals have been banished from the calculus course for reasons of mathematical rigor. Students have had to learn the subject without the original intuition. This calculus book is based on the work of Abraham Robinson, who in 1960 found a way to make infinitesimals rigorous. While the traditional course begins with the difficult limit concept, this course begins with the more easily understood infinitesimals. It is aimed at the average beginning calculus student and covers the usual three or four semester sequence.
The infinitesimal approach has three important advantages for the student. First, it is closer to the intuition which originally led to the calculus. Second, the central concepts of derivative and integral become easier for the student to understand and use. Third, it teaches both the infinitesimal and traditional approaches, giving the student an extra tool which may become increasingly important in the future. Before describing this book, I would like to put Robinsons work in historical perspective. In the 1670s, Leibniz and Newton developed the calculus based on the intuitive notion of infinitesimals.
Infinitesimals were used for another two hundred years, until the first rigorous treatment of the calculus was perfected by Weierstrass in the 1870s. The standard calculus course of today is still based on the 












 TABLE OF INTEGRALS (The constant of integration is left out.)
TABLE OF INTEGRALS (The constant of integration is left out.)  ELEMENTARY ALGEBRA OF THE REAL NUMBERS
ELEMENTARY ALGEBRA OF THE REAL NUMBERS  ALGEBRA OF HYPERREAL NUMBERS Notation:
ALGEBRA OF HYPERREAL NUMBERS Notation: 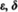 are positive infinitesimals b, c are positive and finite but not infinitesimal H, K are positive infinite. The following are infinitesimal:
are positive infinitesimals b, c are positive and finite but not infinitesimal H, K are positive infinite. The following are infinitesimal: 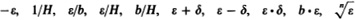 The following are finite but not infinitesimal:
The following are finite but not infinitesimal: 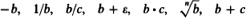 b c is finite (possibly infinitesimal). The following are infinite:
b c is finite (possibly infinitesimal). The following are infinite: 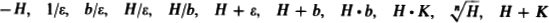 The following can be infinitesimal, finite but not infinitesimal, or infinite:
The following can be infinitesimal, finite but not infinitesimal, or infinite: 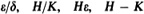 Elementary
Elementary