 ELLIOT MENDELSON is Professor Emeritus of Mathematics at Queens College of the City University of New York. He also has taught at the University of Chicago, Columbia University, and the University of Pennsylvania, and was a member of the Society of Fellows of Harvard University. He is the author of several books, including Schaums Outline of Boolean Algebra and Switching Circuits and Schaums 3000 Solved Problems in Calculus. His principal area of research is mathematical logic and set theory.
ELLIOT MENDELSON is Professor Emeritus of Mathematics at Queens College of the City University of New York. He also has taught at the University of Chicago, Columbia University, and the University of Pennsylvania, and was a member of the Society of Fellows of Harvard University. He is the author of several books, including Schaums Outline of Boolean Algebra and Switching Circuits and Schaums 3000 Solved Problems in Calculus. His principal area of research is mathematical logic and set theory.  Copyright 2008, 1997, 1985 by The McGraw-Hill Companies, Inc. All rights reserved.
Copyright 2008, 1997, 1985 by The McGraw-Hill Companies, Inc. All rights reserved.
Except as permitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. ISBN: 978-0-07-181523-9
MHID: 0-07-181523-6 The material in this eBook also appears in the print version of this title: ISBN: 978-0-07-163535-6, MHID: 0-07-163535-1. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trademarked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringement of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs.
To contact a representative please e-mail us at bulksales@mcgraw-hill.com. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. (McGraw-Hill) and its licensors reserve all rights in and to the work. Use of this work is subject to these terms. Except as permitted under the Copyright Act of 1976 and the right to store and retrieve one copy of the work, you may not decompile, disassemble, reverse engineer, reproduce, modify, create derivative works based upon, transmit, distribute, disseminate, sell, publish or sublicense the work or any part of it without McGraw-Hills prior consent. You may use the work for your own noncommercial and personal use; any other use of the work is strictly prohibited.
Your right to use the work may be terminated if you fail to comply with these terms. THE WORK IS PROVIDED AS IS. McGRAW-HILL AND ITS LICENSORS MAKE NO GUARANTEES OR WARRANTIES AS TO THE ACCURACY, ADEQUACY OR COMPLETENESS OF OR RESULTS TO BE OBTAINED FROM USING THE WORK, INCLUDING ANY INFORMATION THAT CAN BE ACCESSED THROUGH THE WORK VIA HYPERLINK OR OTHERWISE, AND EXPRESSLY DISCLAIM ANY WARRANTY, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. McGraw-Hill and its licensors do not warrant or guarantee that the functions contained in the work will meet your requirements or that its operation will be uninterrupted or error free. Neither McGraw-Hill nor its licensors shall be liable to you or anyone else for any inaccuracy, error or omission, regardless of cause, in the work or for any damages resulting therefrom. McGraw-Hill has no responsibility for the content of any information accessed through the work.
Under no circumstances shall McGraw-Hill and/or its licensors be liable for any indirect, incidental, special, punitive, consequential or similar damages that result from the use of or inability to use the work, even if any of them has been advised of the possibility of such damages. This limitation of liability shall apply to any claim or cause whatsoever whether such claim or cause arises in contract, tort or otherwise.
PREFACE
This Outline is devoted to the essentials of calculus. It carefully develops the principles of differentiation and integration and places special emphasis on the provision of all the steps used in the explanation of the basic ideas and the working out of the solved problems. The book is suitable for reviewing the subject, or as a self-contained text for an elementary calculus course. Because the author has found that many of the difficulties that students encounter in calculus are due to weakness in algebra and arithmetical computation, emphasis has been placed on reviewing algebraic and arithmetical techniques whenever they are used.
Every effort has been madeespecially in regard to the composition of the solved problemsto ease the beginners entry into calculus. There are also well over 1500 supplementary problems (with answers at the end of the book), and many new ones have been added for the Third Edition. In addition to college-level courses, secondary school courses in calculus can readily use this Outline. Many of the problems have been adapted from questions that have appeared in the Advanced Placement Examinations in Calculus, so that students will automatically receive preparation for those tests. A feature of the previous edition that has been carried over is the presence of problems that depend on the availability of graphing calculators. Such problems are preceded by the notation GC, enclosed in a square.
Solution of these problems is not necessary for comprehension of the text (except insofar as the use of a graphing calculator would enhance understanding of the subject). The author is grateful for the help of the many people who provided corrections and suggestions with respect to earlier editions, especially those offered by Frank Cannonito and M. F. Falus. He also wishes to thank the editor of this Third Edition, Charles Wall, as well as the editors of the previous editions, David Beckwith and Arthur Biderman.
CONTENTS
CHAPTER 1
Coordinate Systems on a Line
1.1 THE COORDINATES OF A POINT
Let
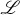
be a line.
Choose a point O on the line and call this point the origin.  Now select a direction along
Now select a direction along 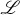 ; say, the direction from left to right on the diagram.
; say, the direction from left to right on the diagram.  For every point P to the right of the origin O, let the coordinate of P be the distance between O and P.
For every point P to the right of the origin O, let the coordinate of P be the distance between O and P.  (Of course, to specify such a distance, it is first necessary to establish a unit distance by arbitrarily picking two points and assigning the number 1 to the distance between these two points.) In the diagram
(Of course, to specify such a distance, it is first necessary to establish a unit distance by arbitrarily picking two points and assigning the number 1 to the distance between these two points.) In the diagram  the distance
the distance 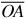 is assumed to be 1, so that the coordinate of A is 1. The point B is two units away from O; therefore, B has coordinate 2. Every positive real number
is assumed to be 1, so that the coordinate of A is 1. The point B is two units away from O; therefore, B has coordinate 2. Every positive real number
Next page






 ELLIOT MENDELSON is Professor Emeritus of Mathematics at Queens College of the City University of New York. He also has taught at the University of Chicago, Columbia University, and the University of Pennsylvania, and was a member of the Society of Fellows of Harvard University. He is the author of several books, including Schaums Outline of Boolean Algebra and Switching Circuits and Schaums 3000 Solved Problems in Calculus. His principal area of research is mathematical logic and set theory.
ELLIOT MENDELSON is Professor Emeritus of Mathematics at Queens College of the City University of New York. He also has taught at the University of Chicago, Columbia University, and the University of Pennsylvania, and was a member of the Society of Fellows of Harvard University. He is the author of several books, including Schaums Outline of Boolean Algebra and Switching Circuits and Schaums 3000 Solved Problems in Calculus. His principal area of research is mathematical logic and set theory.  Copyright 2008, 1997, 1985 by The McGraw-Hill Companies, Inc. All rights reserved.
Copyright 2008, 1997, 1985 by The McGraw-Hill Companies, Inc. All rights reserved.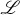 be a line.
be a line.  Now select a direction along
Now select a direction along  For every point P to the right of the origin O, let the coordinate of P be the distance between O and P.
For every point P to the right of the origin O, let the coordinate of P be the distance between O and P.  (Of course, to specify such a distance, it is first necessary to establish a unit distance by arbitrarily picking two points and assigning the number 1 to the distance between these two points.) In the diagram
(Of course, to specify such a distance, it is first necessary to establish a unit distance by arbitrarily picking two points and assigning the number 1 to the distance between these two points.) In the diagram  the distance
the distance 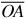 is assumed to be 1, so that the coordinate of A is 1. The point B is two units away from O; therefore, B has coordinate 2. Every positive real number
is assumed to be 1, so that the coordinate of A is 1. The point B is two units away from O; therefore, B has coordinate 2. Every positive real number