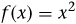How to Solve Word Problems in Calculus A Solved Problem Approach Other books in the How to Solve Word Problems series: How to Solve Word Problems in Algebra How to Solve Word Problems in Arithmetic How to Solve Word Problems in Chemistry How to Solve Word Problems in Geometry How to Solve Word Problems in Mathematics  Dedicated to our past and future:
Dedicated to our past and future:
Jack, Leo, Alexis, and Ariel
Contents
Preface
This book is designed to enable students of calculus to develop their skills in solving word problems. Most calculus textbooks present this topic in a cursory manner, forcing the student to struggle with the techniques of setting up and solving complex verbal problems. This book, which may be used as a supplement to all calculus textbooks, is presented in a manner that has proved so successful with the other books in the
How to Solve Word Problems series: Concise definitions and discussion of appropriate theory in easily understood terms. Fully worked out solutions to illustrative examples. Supplementary problems with complete solutions. The purpose of this book is to increase the students confidence in his or her ability to solve word problems.
The material is presented in an easy-to-understand, readable manner and if the reader is willing to invest a little time and effort, he or she will be rewarded with a skill which will prove invaluable. EUGENE DON
BENAY DON
Introduction
Strategies for Solving Word Problems
The power of calculus lies in its ability to solve applied problems in such diverse areas as physics, chemistry, biology, business, economics, and the social sciences. Invariably, human beings, using
words that attempt to describe some realistic situation, pose such problems. This book addresses the difficulties many students have solving word problems in their calculus courses. The first task in solving a word problem is to develop a
model for the problem at hand. A mathematical model is a description of the problem in terms of variables, functions, equations, and other mathematical entities.
Once it has been modeled, the second task is to solve the problem using the appropriate mathematical tools. Setting up and solving a calculus problem from a verbal description is a skill, which is best learned by example, following appropriate guidelines. By studying the steps set forth in each chapter, you will develop techniques that can be applied to a variety of different applications. Try to avoid memorizing procedures applicable only to specific problems. Although this will give you instant gratification when you get the correct answer, you will find that if a problem deviates even slightly from the one you memorized, you will be hopelessly lost. A better approach is to learn general procedures, which can be applied to all problems within a specific category.
Reading a word problem is not like reading a novel. Every word is important and must be clearly understood if you are to successfully arrive at the solution. Feel free to use a dictionary, if necessary, to clarify the meaning of seemingly vague words. Use your math book to clarify the meaning of any technical words used in the problem. Read and re-read the problem until it is absolutely clear what you are given and what it is you are looking for. Then, and only then, should you begin the solution.
This book contains many worked out examples. However, you must understand that there is a big difference between viewing the solution of a problem and solving the problem by yourself. When you read an example in this book, you may be able to follow every step but you should not be misled into thinking that you completely understand the solution. Learning to solve problems is like learning to play a musical instrument. You may think a musical selection is simple while watching your teacher play it with ease, but it is not until you attempt the piece yourself that you begin to see what technical difficulties actually lie within the music. One suggestion, which you might find useful, is to pick a problem from this book and read the solution.
When you think you understand what you have read, cover the solution and attempt the problem yourself. Most likely you will find that you have some difficulty. If you have trouble sneak a peek at the solution to determine the step that caused you difficulty. Then cover the solution again and continue. Repeat this process every time you get stuck. When you finally get to the end, take a deep breath and then attempt the problem again from the beginning.
You have truly mastered the problem only if you can go from the beginning to the end by yourself without looking at the authors solution. Solving word problems is more of an art than a science. Like all artistic endeavors, perfection takes practice, patience, and perseverance. You may be frustrated at first but if you follow the guidelines described in this book, you will master this all-important skill.
Chapter 1
Extracting Functions from Word Problems
Calculus is the study of the behavior of
functions. The ability to solve real life problems using calculus hinges upon the ability to extract a function from a given description or physical situation.
Students usually find that a word problem is easily solved once the underlying mathematical function is determined. In this chapter we discuss techniques that will form the basis for solving a variety of word problems encountered in calculus courses. One definition of a function found in calculus texts reads: A function is a rule that assigns to each number x A, a unique number y B. In calculus, A and B are sets of real numbers. A is called the domain and B the range. It is important to understand that a function is not a number, but a correspondence between two sets of numbers.
In a practical sense, one may think of a function as a relationship between y and x. The important thing is that there be one, and only one, value of y corresponding to a given value of x. EXAMPLE 1 If 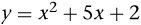 , then y is a function of x. For each value of x there is clearly one and only one value of y. However, if the equation
, then y is a function of x. For each value of x there is clearly one and only one value of y. However, if the equation 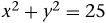 defines the correspondence between x and y, then y is not a function of x. If
defines the correspondence between x and y, then y is not a function of x. If 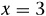 , for example, then y could be 4 or 4.
, for example, then y could be 4 or 4.
Functions are usually represented symbolically by a letter such as f or g. For convenience, function notation is often used in calculus. In terms of the definition above, if f is a function and x A, then f(x) is the unique number in B corresponding to x. It is not uncommon to use a letter that reminds us of what a function represents. Thus for example, A(x) may be used to represent the area of a square whose side is x or V(r) may represent the volume of a sphere whose radius is r. EXAMPLE 2 Suppose f represents the squaring function, i.e., the function that squares x.
We write 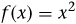
Next page









 Dedicated to our past and future:
Dedicated to our past and future: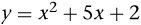 , then y is a function of x. For each value of x there is clearly one and only one value of y. However, if the equation
, then y is a function of x. For each value of x there is clearly one and only one value of y. However, if the equation 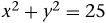 defines the correspondence between x and y, then y is not a function of x. If
defines the correspondence between x and y, then y is not a function of x. If 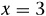 , for example, then y could be 4 or 4.
, for example, then y could be 4 or 4.