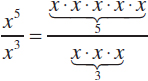Attacking Problems in Logarithms and Exponential Functions
David S. Kahn
DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright
Copyright 2015 by David S. Kahn
All rights reserved.
Bibliographical Note
Attacking Problems in Logarithms and Exponential Functions is a new work, first published by Dover Publications, Inc., in 2015.
Library of Congress Cataloging-in-Publication Data
Kahn, David S.
Attacking problems in logarithms and exponential functions / David S. Kahn.
p. cm.
eISBN-13: 978-0-486-80801-7
1. Exponents (Algebra)Textbooks. 2. Logarithmic functionsTextbooks. I. Title.
QA161. E95E97 2014
512.922076dc23
2015021790
Manufactured in the United States by RR Donnelley
79346X01 2015
www.doverpublications.com
To the Reader:
Logarithms and exponential functions are topics that students usually encounter in Precalculus, or sometimes in Advanced Algebra. They are of crucial importance to understand both higher mathematics and all of the sciences, as well as Economics, Finance, and a host of other topics. Fortunately, they are not that difficult to master, with a little diligence and patience. Thanks to the book that you are about to use, you will be able to attack logarithms and exponential functions and successfully conquer them.
One of the keys to doing well in these areas is to be comfortable with graphing and with algebraic manipulation. Logarithms and exponential functions require an understanding of how a function grows, and this will be easy for you to understand when you picture the graph. You will also learn to solve equations with logarithms or containing exponentials, and the algebra is not that hard. Sometimes we will show you all of the steps to a solution; other times, we will leave you to work them out on your own. If you are not already good at factoring a quadratic equation, or working with distributing and rearranging terms, we suggest that you practice those topics. It will make this book much easier to use!
Another key to doing well is to drill. It is important to be able to work with logarithms, which is not nearly as scary as it might sound, and it will be much easier if you do all of the practice problems to reinforce the concepts. If you do so, you will find that logarithms and exponential functions are not so hard after all.
We have organized this book so that you can proceed from one topic to another, or you can jump to the topics that you want to work on. The book is divided into ten units, each of which will teach you what you need to know to do well in that topic. This is not designed to be an exhaustive treatise on logarithms or exponential functions, nor is it designed to be a textbook. Rather, this book focuses on the essentials and how to get the problems right. We suggest that you read through each unit completely and do all of the exercises and practice problems. Each example and problem has a complete explanation to help you understand how to solve the problem correctly. After you have worked through a unit, if you still want more practice problems, you may want to go to a textbook.
Logarithms and exponential functions are a highly valuable and useful area of mathematics. After you have gone through this book, you will be able to handle with ease problems involving logarithms and exponents on your exams, and apply this knowledge to mathematics, the sciences, the social sciences, and business. Are you ready? Then its time to Attack Logarithms and Exponential Functions!
Acknowledgments
First of all, I would like to thank Nicole Maisonet for her excellent drawings. It is a tedious task and she did it with grace and enthusiasm. Next, I would like to thank Magan Farraj for working through all of the problems, double-checking my calculations. I owe a lifetime debt to my father, Peter Kahn, and to my dear friend, Arnold Feingold, who encouraged my interest in Mathematics and have always been there to guide me through the rough spots. And finally, I would like to thank the very many students whom I have taught and tutored, who never hesitate to correct me when I am wrong, and who provide the fulfillment that I so deeply derive from teaching math.
Attacking Problems in Logarithms and Exponential Functions
UNIT ONE
Seven Simple Rules for Working with Exponents
When we multiply a number by itself, we call this process squaring. For example, when we multiply 33 = 9 we use a short-hand method. We write the expression as 32, where the 2 indicates that we have multiplied the number by itself 2 times. So, if we wrote 33, that would indicate that we have multiplied the number by itself 3 times, that is, 333 = 27. Similarly, 34 = 3333 = 81, and so on. Thus, 56 = 555555 = 15,625. Got the idea?
Notice how quickly the result grows when we multiply a number by itself. For example, we only had to multiply 5 by itself 6 times to get 15,625. Think about what this means. If we had 5 people in a room, and each of them brought 5 friends into the room, we would have 52 = 25 people. If we now had each of those people bring in 5 friends, we would have 53 = 125 people. If we then repeated the process three more times, we would have 15,625 people. We would need a very big room! This is the essential fact of exponential growth, which we will explore in this book. Namely, that one can start with a small number and, in just a few steps, end up with a very large number.
Now lets figure out some rules about exponents. What does it mean to raise a number to the power of 1? Lets see. If we write 41, we multiply 4 one time. That is, 41 = 4. Now lets dispense with using numbers. If we write x1, we multiply x, one time, so x1 = x.
Now, what if we raise x to the power a. This means that we multiply x by itself a times.
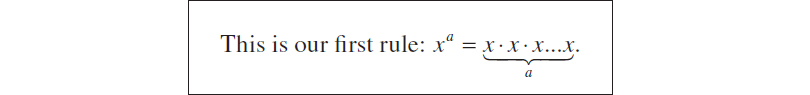
Now suppose we have two expressions, x3 and x5. What happens when we multiply them together? Remember that x3 = xxx and x5 = xxxxx, so if we multiply them, we get 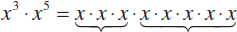 . We have x multiplied by itself 8 times, so x3x5 = x8. Now lets do this again, but this time with xa and xb. If we multiply them, we get
. We have x multiplied by itself 8 times, so x3x5 = x8. Now lets do this again, but this time with xa and xb. If we multiply them, we get 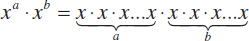 . Thus,
. Thus, 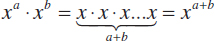 .
.

Notice that this requires that the two expressions have the same base, namely x. What if you have xayb? You cant do anything with this expression. For example, if you have 53 42, you have to evaluate each separately to get 53 = 125 and 42 = 16, and thus 53 42 = 125 16 = 2000.
By the way, if you have 52 42 instead, you could evaluate them separately: 52 = 25 and 42 = 16. So 52 42 = 25 16 = 400, or you could combine them into (54)2 = 202 = 400. This means that xa ya = (xy)a. Be careful when you combine expressions with different bases!
Suppose that, instead of multiplying x5 and x3, we divide them. We get 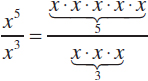
Next page












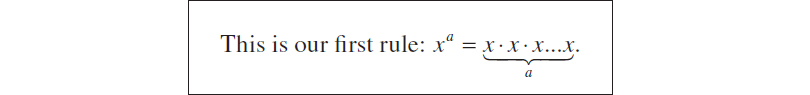
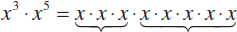 . We have x multiplied by itself 8 times, so x3x5 = x8. Now lets do this again, but this time with xa and xb. If we multiply them, we get
. We have x multiplied by itself 8 times, so x3x5 = x8. Now lets do this again, but this time with xa and xb. If we multiply them, we get 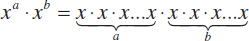 . Thus,
. Thus, 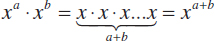 .
.