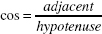ATTACKING
TRIGONOMETRY
PROBLEMS
David S. Kahn DOVER PUBLICATIONS, INC.
Mineola, New York
Copyright Copyright 2015 by David S. Kahn All rights reserved.
Bibliographical NoteAttacking Trigonometry Problems is a new work, first published by Dover Publications, Inc., in 2015.
International Standard Book NumbereISBN-13: 978-0-486-80479-8 Manufactured in the United States by Courier Corporation 78967501 2015
www.doverpublications.com
To the Reader:
Welcome to trigonometry! If you are like most students, this is the last mathematics course that you will have to take before calculus, or in some cases, ever! One of the difficulties of trigonometry is that you will have to combine several of the skills that you have developed in previous classes, namely, geometry, algebra, and graphing. Furthermore, you will have to use both of these in algebraic problems and in word problems.
This may sound intimidating, but it doesnt have to be. Trigonometry can be challenging, but that doesnt mean that you cant handle it. Thanks to the book that you are about to use, you will be able to attack trigonometry and successfully conquer it. One of the keys to doing well in trigonometry is memorizing. We recognize that many of you are not excited about the idea of memorizing the various ratios and formulas, but you will find that you will do much better, and have an easier time with trig, if you do. We will point out in the text what you need to memorize.
We suggest that you do so! Another key is to drill. This goes along with memorization. It is important to get comfortable with using the trig ratios in a variety of ways, and it will be much easier if you do all of the practice problems to reinforce the concepts. If you do so, you will find that trig isnt so hard after all. We have organized this book so that you can proceed from one topic of trig to another, or you can jump to the topics that you want to work on. The book is divided into 14 units, each of which will teach you what you need to know to do well in that topic.
This is not designed to be an exhaustive treatise on trigonometry, nor is it designed to be a textbook. Rather, this book focuses on the essentials, and how to master the problems. We suggest that you read through each unit completely, do all of the exercises, and complete all of the practice problems. Each example and problem has a complete explanation to help you understand how to solve the problem correctly. There are many good textbooks on trigonometry, and after you have worked through a unit, you may want to refer to a textbook for further practice. Trigonometry can be a fun and useful area of mathematics.
After you have gone through this book, you will be able to handle the trig on your exams with ease, and you will be prepared for calculus. Are you ready? Then its time to Attack Trigonometry!
Acknowledgments
First of all, I would like to thank Nicole Maisonet for her excellent drawings. It is a tedious task and she did it with grace and enthusiasm. Next, I would like to thank Magan Farraj for working through all of the problems, double-checking my calculations. I owe a lifetime debt to my father, Peter Kahn, and to my dear friend, Arnold Feingold, who encouraged my interest in Mathematics and have always been there to guide me through the rough spots. And finally, I would like to thank the very many students whom I have taught and tutored, who have never hesitated to correct me when I am wrong, and who provide the fulfillment that I so deeply derive from teaching math.
ATTACKING
TRIGONOMETRY
PROBLEMS
UNIT ONE
The Basic Trig Ratios
Trigonometry consists of learning how to use six different functions, or ratios, which show up in a surprisingly large number of places. Where do they come from? A good place to start is with some basic geometry. Remember similar triangles? If two triangles are similar, then they have equal angles and the ratio of their sides is the same. For example,
Figure 1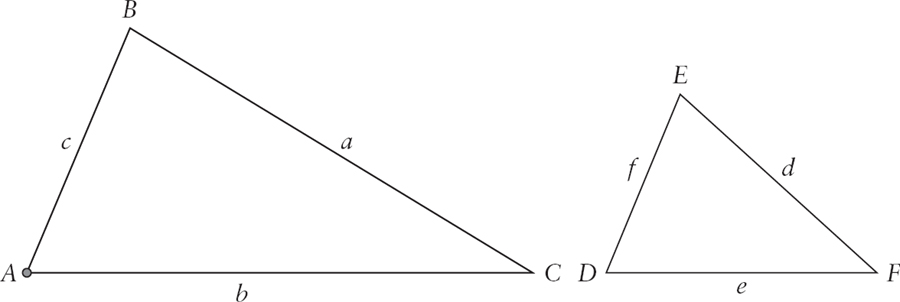
If the two triangles above are similar, then
A =
D,
B =
E, and
C =
F, and
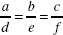
. Lets look at two similar right triangles:
Figure 2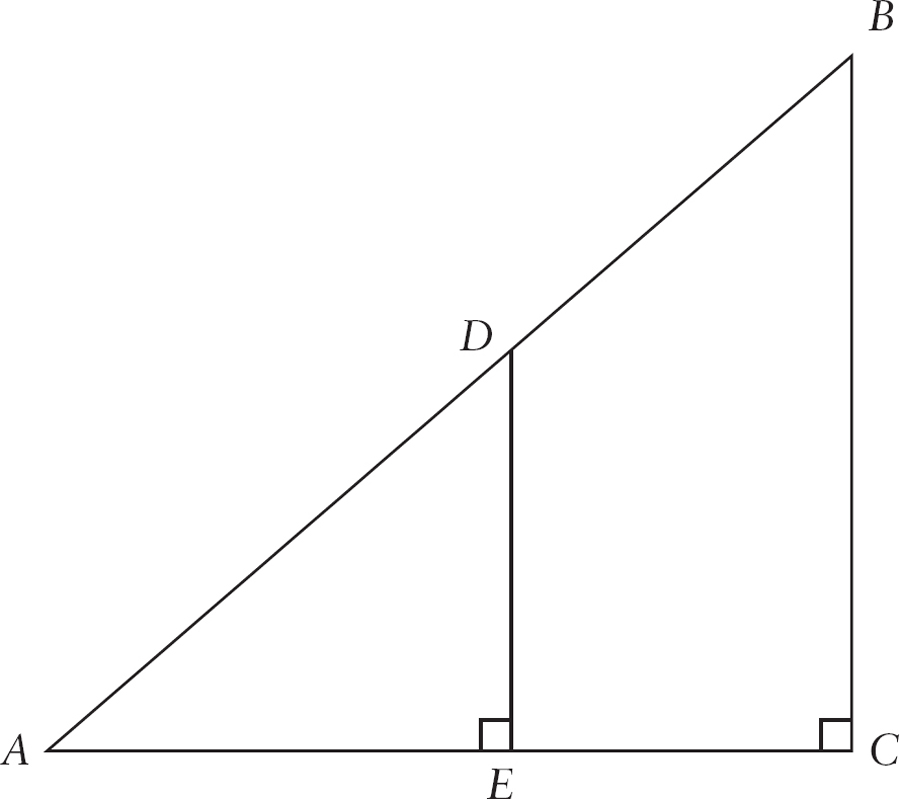
Notice that
ABC is similar to
ADE because each contains a right angle (
C & E) and the same angle (
A), and so the third angle must also be the same (because the measures of the angles in a triangle add to 180). This means that
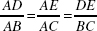
.
If we had the following set of right triangles, the corresponding ratios would all be equal. Figure 3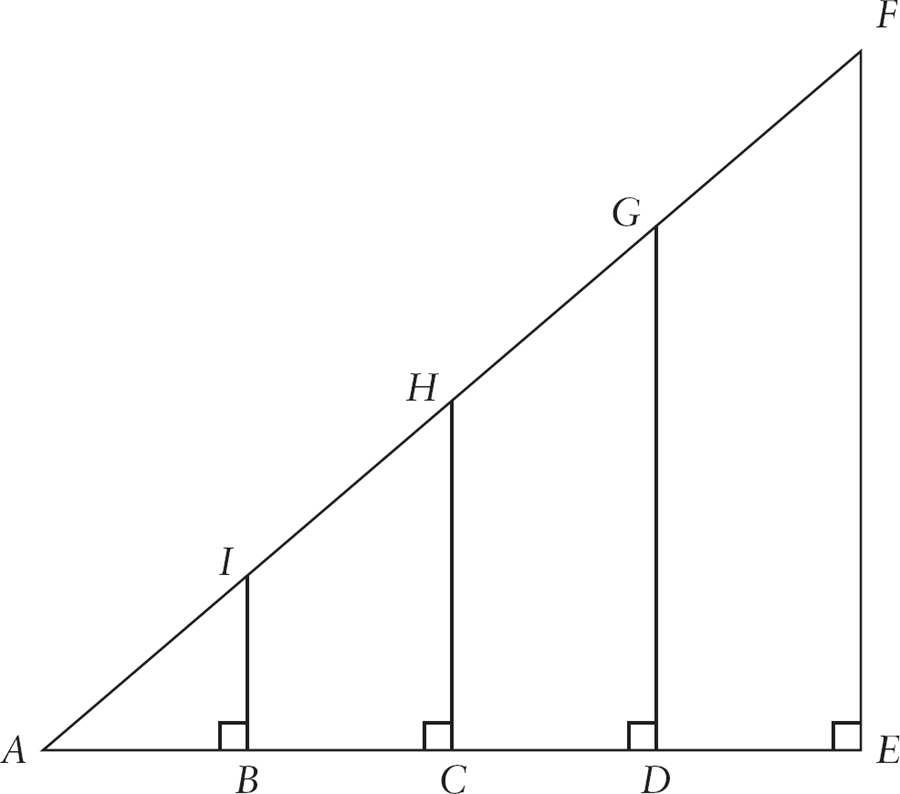 In fact, for any right triangle that has an angle with a measure equal to the measure of angle A, the ratios are the same as those of any other right triangle that has an angle with measure equal to that of A. This is the essential fact of Trigonometry and can be used in many powerful ways. For the triangle below, these are the three basic trigonometric ratios to learn: Figure 4
In fact, for any right triangle that has an angle with a measure equal to the measure of angle A, the ratios are the same as those of any other right triangle that has an angle with measure equal to that of A. This is the essential fact of Trigonometry and can be used in many powerful ways. For the triangle below, these are the three basic trigonometric ratios to learn: Figure 4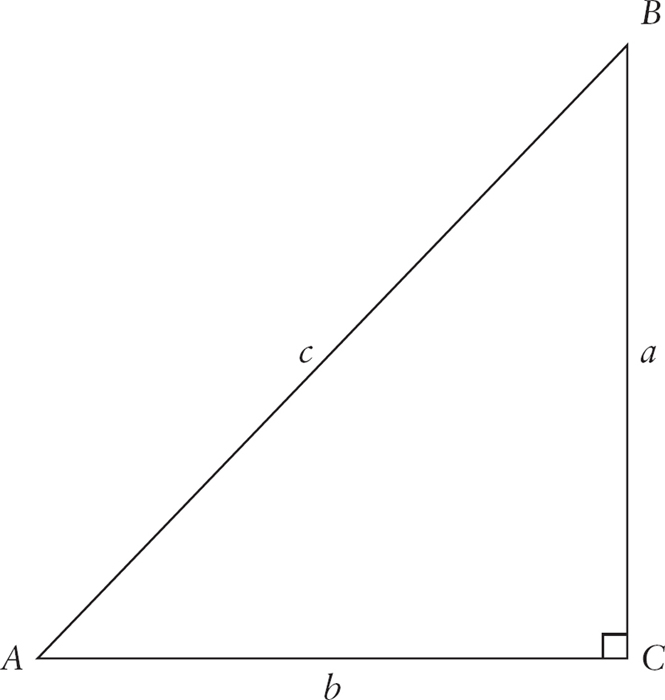 The sine of angle A is the ratio
The sine of angle A is the ratio  . The cosine of angle A is the ratio
. The cosine of angle A is the ratio  . The tangent of angle A is the ratio
. The tangent of angle A is the ratio  .
.
We usually abbreviate sine as sin, cosine as cos, and tangent as tan, and write these ratios using the following notation: 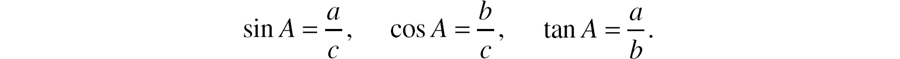 You will want to get comfortable with these ratios. There is an easy way to memorize them. Figure 5
You will want to get comfortable with these ratios. There is an easy way to memorize them. Figure 5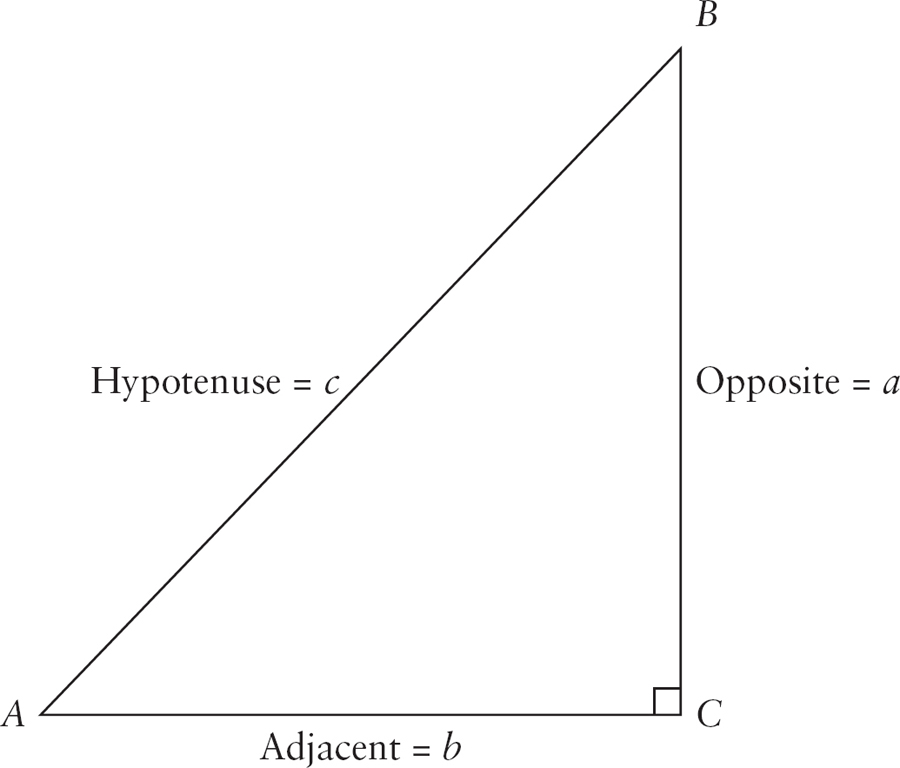 There are three sides from the perspective of angle A: a is the side opposite angle A, b is the side adjacent to angle A, and c is the hypotenuse. Therefore, we can think of:
There are three sides from the perspective of angle A: a is the side opposite angle A, b is the side adjacent to angle A, and c is the hypotenuse. Therefore, we can think of:  This gives the traditional mnemonic: SOH CAH TOA which stands for:
This gives the traditional mnemonic: SOH CAH TOA which stands for: 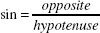 ,
, 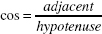

















 If the two triangles above are similar, then A = D, B = E, and C = F, and
If the two triangles above are similar, then A = D, B = E, and C = F, and 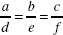 . Lets look at two similar right triangles: Figure 2
. Lets look at two similar right triangles: Figure 2 Notice that ABC is similar to ADE because each contains a right angle (C & E) and the same angle (A), and so the third angle must also be the same (because the measures of the angles in a triangle add to 180). This means that
Notice that ABC is similar to ADE because each contains a right angle (C & E) and the same angle (A), and so the third angle must also be the same (because the measures of the angles in a triangle add to 180). This means that 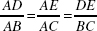 .
.  In fact, for any right triangle that has an angle with a measure equal to the measure of angle A, the ratios are the same as those of any other right triangle that has an angle with measure equal to that of A. This is the essential fact of Trigonometry and can be used in many powerful ways. For the triangle below, these are the three basic trigonometric ratios to learn: Figure 4
In fact, for any right triangle that has an angle with a measure equal to the measure of angle A, the ratios are the same as those of any other right triangle that has an angle with measure equal to that of A. This is the essential fact of Trigonometry and can be used in many powerful ways. For the triangle below, these are the three basic trigonometric ratios to learn: Figure 4 The sine of angle A is the ratio
The sine of angle A is the ratio  . The cosine of angle A is the ratio
. The cosine of angle A is the ratio  . The tangent of angle A is the ratio
. The tangent of angle A is the ratio  .
.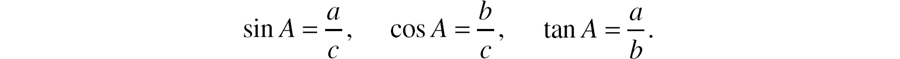 You will want to get comfortable with these ratios. There is an easy way to memorize them. Figure 5
You will want to get comfortable with these ratios. There is an easy way to memorize them. Figure 5 There are three sides from the perspective of angle A: a is the side opposite angle A, b is the side adjacent to angle A, and c is the hypotenuse. Therefore, we can think of:
There are three sides from the perspective of angle A: a is the side opposite angle A, b is the side adjacent to angle A, and c is the hypotenuse. Therefore, we can think of:  This gives the traditional mnemonic: SOH CAH TOA which stands for:
This gives the traditional mnemonic: SOH CAH TOA which stands for: 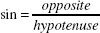 ,
,