Mary Jane Sterling - Trigonometry for Dummies

Trigonometry For Dummies, 2nd Edition

Published by: John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030-5774, www.wiley.com

Copyright 2014 by John Wiley & Sons, Inc., Hoboken, New Jersey

Published simultaneously in Canada

No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without the prior written permission of the Publisher. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permissions .

Trademarks: Wiley, For Dummies, the Dummies Man logo, Dummies.com, Making Everything Easier, and related trade dress are trademarks or registered trademarks of John Wiley & Sons, Inc., and may not be used without written permission. All other trademarks are the property of their respective owners. John Wiley & Sons, Inc., is not associated with any product or vendor mentioned in this book.

LIMIT OF LIABILITY/DISCLAIMER OF WARRANTY : WHILE THE PUBLISHER AND AUTHOR HAVE USED THEIR BEST EFFORTS IN PREPARING THIS BOOK, THEY MAKE NO REPRESENTATIONS OR WARRANTIES WITH RESPECT TO THE ACCURACY OR COMPLETENESS OF THE CONTENTS OF THIS BOOK AND SPECIFICALLY DISCLAIM ANY IMPLIED WARRANTIES OF MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. NO WARRANTY MAY BE CREATED OR EXTENDED BY SALES REPRESENTATIVES OR WRITTEN SALES MATERIALS. THE ADVICE AND STRATEGIES CONTAINED HEREIN MAY NOT BE SUITABLE FOR YOUR SITUATION. YOU SHOULD CONSULT WITH A PROFESSIONAL WHERE APPROPRIATE. NEITHER THE PUBLISHER NOR THE AUTHOR SHALL BE LIABLE FOR DAMAGES ARISING HEREFROM.

For general information on our other products and services, please contact our Customer Care Department within the U.S. at 877-762-2974, outside the U.S. at 317-572-3993, or fax 317-572-4002. For technical support, please visit www.wiley.com/techsupport .

Wiley publishes in a variety of print and electronic formats and by print-on-demand. Some material included with standard print versions of this book may not be included in e-books or in print-on-demand. If this book refers to media such as a CD or DVD that is not included in the version you purchased, you may download this material at http://booksupport.wiley.com . For more information about Wiley products, visit www.wiley.com .

Library of Congress Control Number: 2013954199

ISBN 978-1-118-82741-3 (pbk); ISBN 978-1-118-82746-8 (ebk); ISBN 978-1-118-82757-4 (ebk)

Manufactured in the United States of America

10 9 8 7 6 5 4 3 2 1

Chapter 1

In This Chapter

Understanding what trigonometry is

Speaking the language by defining the words

Writing trig functions as equations

Graphing for understanding

H ow did Columbus find his way across the Atlantic Ocean? How did the Egyptians build the pyramids? How did early astronomers measure the distance to the moon? No, Columbus didn't follow a yellow brick road. No, the Egyptians didn't have LEGO instructions. And, no, there isn't a tape measure long enough to get to the moon. The common answer to all these questions is trigonometry.

Trigonometry is the study of angles and triangles and the wonderful things about them and that you can do with them. For centuries, humans have been able to measure distances that they can't reach because of the power of this mathematical subject.

What's your angle? That question isn't a come-on such as What's your astrological sign? In trigonometry, you measure angles in both degrees and radians. You can shove the angles into triangles and circles and make them do special things. Actually, angles drive trigonometry. Sure, you have to consider algebra and other math to make it all work. But you can't have trigonometry without angles. Put an angle into a trig function, and out pops a special, unique number. What do you do with that number? Read on, because that's what trig is all about.

Segments, rays, and lines are some of the basic forms found in geometry, and they're almost as important in trigonometry. As I explain in the following sections, you use those segments, rays, and lines to form angles.

A segment is a straight figure drawn between two endpoints. You usually name it by its endpoints, which you indicate by capital letters. Sometimes, a single letter names a segment. For example, in a triangle, a lowercase letter may refer to a segment opposite the angle labeled with the corresponding uppercase letter.

A ray is another straight figure that has an endpoint on one end, and then it just keeps going forever in some specified direction. You name rays by their endpoint first and then by any other point that lies on the ray.

A line is a straight figure that goes forever and ever in either direction. You only need two points to determine a particular line and only one line can go through both of those points. You can name a line by any two points that lie on it.

Figure shows a segment, ray, and line and the different ways you can name them using points.

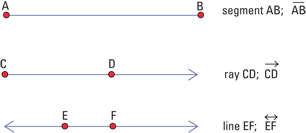
Figure 1-1: Segment AB, ray CD, and line EF.

Intersecting lines

When two lines intersect if they do intersect they can only do so at one point. They can't double back and cross one another again. And some curious things happen when two lines intersect. The angles that form between those two lines are related to one another. Any two angles that are next to one another and share a side are called adjacent angles. In Figure , the two middle figures indicate the only pairs of vertical angles. Vertical angles are always equal in measure.

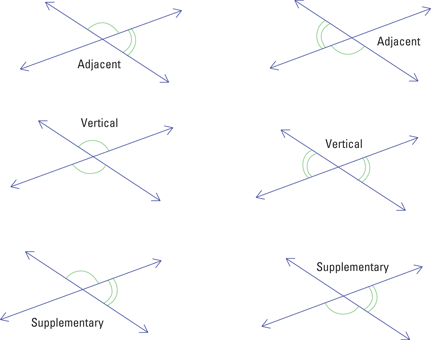
Figure 1-2: Intersecting lines form adjacent, vertical, and supplementary angles.

Why are these different angles so special? They're different because of how they interact with one another. The adjacent angles here are called supplementary angles. The sides that they don't share form a straight line, which has a measure of 180 degrees. The bottom two figures show supplementary angles. Note that these are also adjacent.

Angling for position

When two lines, segments, or rays touch or cross one another, they form an angle or angles. In the case of two intersecting lines, the result is four different angles. When two segments intersect, they can form one, two, or four angles; the same goes for two rays.

These examples are just some of the ways that you can form angles. Geometry, for example, describes an angle as being created when two rays have a common endpoint. In practical terms, you can form an angle in many ways, from many figures. The business with the two rays means that you can extend the two sides of an angle out farther to help with measurements, calculations, and practical problems.