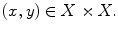Adam Bowers - An Introductory Course in Functional Analysis
Here you can read online Adam Bowers - An Introductory Course in Functional Analysis full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:An Introductory Course in Functional Analysis
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
An Introductory Course in Functional Analysis: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "An Introductory Course in Functional Analysis" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Based on a graduate course by the celebrated analyst Nigel Kalton, this well-balanced introduction to functional analysis makes clear not only how, but why, the field developed. All major topics belonging to a first course in functional analysis are covered. However, unlike traditional introductions to the subject, Banach spaces are emphasized over Hilbert spaces, and many details are presented in a novel manner, such as the proof of the HahnBanach theorem based on an inf-convolution technique, the proof of Schauders theorem, and the proof of the MilmanPettis theorem.
With the inclusion of many illustrative examples and exercises, An Introductory Course in Functional Analysis equips the reader to apply the theory and to master its subtleties. It is therefore well-suited as a textbook for a one- or two-semester introductory course in functional analysis or as a companion for independent study.
Adam Bowers: author's other books
Who wrote An Introductory Course in Functional Analysis? Find out the surname, the name of the author of the book and a list of all author's works by series.






![Eisner Tanja - Operator Theoretic Aspects of Ergodic Theory [recurso electrónico] $c](/uploads/posts/book/173124/thumbs/eisner-tanja-operator-theoretic-aspects-of.jpg)







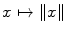 defined for all
defined for all 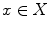 , called a norm , such that
, called a norm , such that 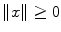 for all
for all 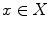 , and
, and 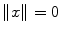 if and only if x =0,
if and only if x =0,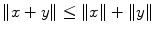 for all x and y in X , and
for all x and y in X , and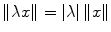 for all
for all 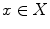 and scalars .
and scalars .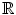 (or
(or 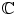 ), the norm of x is given by the absolute value (or modulus) of x , which is denoted (in either case) by
), the norm of x is given by the absolute value (or modulus) of x , which is denoted (in either case) by 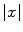 .
.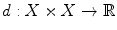 that satisfies the following properties:
that satisfies the following properties: 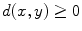 for all x and y in X , and
for all x and y in X , and 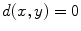 if and only if x=y ,
if and only if x=y ,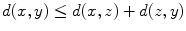 for all x , y , and z in X , and
for all x , y , and z in X , and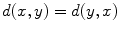 for all x and y in X .
for all x and y in X .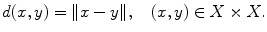
 in X is said to converge to a point x in X if for any
in X is said to converge to a point x in X if for any  there exists an
there exists an 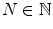 such that
such that 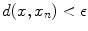 whenever
whenever 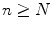 . In such a case, we say the sequence is convergent and write
. In such a case, we say the sequence is convergent and write 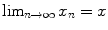 . A sequence
. A sequence 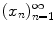 in X is called a Cauchy sequence if for any
in X is called a Cauchy sequence if for any 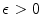 there exists an
there exists an 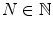 such that
such that 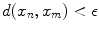 whenever
whenever 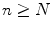 and
and 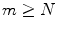 .
.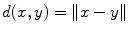 for all
for all