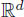Elias M. Stein - Functional Analysis: Introduction to Further Topics in Analysis: Bk. 4

FUNCTIONAL ANALYSIS

Princeton Lectures in Analysis

I Fourier Analysis: An Introduction

II Complex Analysis

III Real Analysis: Measure Theory,
Integration, and Hilbert Spaces

IV Functional Analysis: Introduction
to Further Topics in Analysis

PRINCETON LECTURES IN ANALYSIS

IV

INTRODUCTION TO FURTHER TOPICS IN
ANALYSIS

Elias M. Stein
&
Rami Shakarchi

Copyright 2011 by Princeton University Press

Published by Princeton University Press

41 William Street, Princeton, New Jersey 08540

In the United Kingdom: Princeton University Press

6 Oxford Street, Woodstock, Oxfordshire, OX20 1TW

All Rights Reserved

Library of Congress Cataloging-in-Publication Data is available

ISBN 978-0-691-11387-6

British Library Cataloging-in-Publication Data is available

This book has been composed in

The publisher would like to acknowledge the authors of this volume for providing the camera-ready copy from which this book was printed.

Printed on acid-free paper.

press.princeton.edu

Printed in the United States of America

10 9 8 7 6 5 4 3 2 1

TO MY GRANDCHILDREN

CAROLYN, ALISON, JASON

E.M.S.

TO MY PARENTS

MOHAMED & MIREILLE

AND MY BROTHER

KARIM

R.S.

Beginning in the spring of 2000, a series of four one-semester courses were taught at Princeton University whose purpose was to present, in an integrated manner, the core areas of analysis. The objective was to make plain the organic unity that exists between the various parts of the subject, and to illustrate the wide applicability of ideas of analysis to other fields of mathematics and science. The present series of books is an elaboration of the lectures that were given.

While there are a number of excellent texts dealing with individual parts of what we cover, our exposition aims at a different goal: presenting the various sub-areas of analysis not as separate disciplines, but rather as highly interconnected. It is our view that seeing these relations and their resulting synergies will motivate the reader to attain a better understanding of the subject as a whole. With this outcome in mind, we have concentrated on the main ideas and theorems that have shaped the field (sometimes sacrificing a more systematic approach), and we have been sensitive to the historical order in which the logic of the subject developed.

We have organized our exposition into four volumes, each reflecting the material covered in a semester. Their contents may be broadly summarized as follows:

I. Fourier series and integrals.

II. Complex analysis.

III. Measure theory, Lebesgue integration, and Hilbert spaces.

IV. A selection of further topics, including functional analysis, distributions, and elements of probability theory.

However, this listing does not by itself give a complete picture of the many interconnections that are presented, nor of the applications to other branches that are highlighted. To give a few examples: the elements of (finite) Fourier series studied in Book I, which lead to Dirichlet characters, and from there to the infinitude of primes in an arithmetic progression; the X-ray and Radon transforms, which arise in a number of problems in Book I, and reappear in Book III to play an important role in understanding Besicovitch-like sets in two and three dimensions; Fatous theorem, which guarantees the existence of boundary values of bounded holomorphic functions in the disc, and whose proof relies on ideas developed in each of the first three books; and the theta function, which first occurs in Book I in the solution of the heat equation, and is then used in Book II to find the number of ways an integer can be represented as the sum of two or four squares, and in the analytic continuation of the zeta function.

A few further words about the books and the courses on which they were based. These courses where given at a rather intensive pace, with 48 lecture-hours a semester. The weekly problem sets played an indispensable part, and as a result exercises and problems have a similarly important role in our books. Each chapter has a series of Exercises that are tied directly to the text, and while some are easy, others may require more effort. However, the substantial number of hints that are given should enable the reader to attack most exercises. There are also more involved and challenging Problems; the ones that are most difficult, or go beyond the scope of the text, are marked with an asterisk.

Despite the substantial connections that exist between the different volumes, enough overlapping material has been provided so that each of the first three books requires only minimal prerequisites: acquaintance with elementary topics in analysis such as limits, series, differentiable functions, and Riemann integration, together with some exposure to linear algebra. This makes these books accessible to students interested in such diverse disciplines as mathematics, physics, engineering, and finance, at both the undergraduate and graduate level.

It is with great pleasure that we express our appreciation to all who have aided in this enterprise. We are particularly grateful to the students who participated in the four courses. Their continuing interest, enthusiasm, and dedication provided the encouragement that made this project possible. We also wish to thank Adrian Banner and Jos Luis Rodrigo for their special help in running the courses, and their efforts to see that the students got the most from each class. In addition, Adrian Banner also made valuable suggestions that are incorporated in the text.

We wish also to record a note of special thanks for the following individuals: Charles Fefferman, who taught the first week (successfully launching the whole project!); Paul Hagelstein, who in addition to reading part of the manuscript taught several weeks of one of the courses, and has since taken over the teaching of the second round of the series; and Daniel Levine, who gave valuable help in proofreading. Last but not least, our thanks go to Gerree Pecht, for her consummate skill in type-setting and for the time and energy she spent in the preparation of all aspects of the lectures, such as transparencies, notes, and the manuscript.

We are also happy to acknowledge our indebtedness for the support we received from the 250th Anniversary Fund of Princeton University, and the National Science Foundations VIGRE program.

Elias M. Stein
Rami Shakarchi

Princeton, New Jersey
August 2002

As with the previous volumes, we are happy to record our great debt to Daniel Levine. The final version of this book has been much improved because of his help. He read the entire manuscript with great care and made valuable suggestions that have been incorporated in the text. We also wish to take this opportunity to thank Hart Smith and Polam Yung for proofreading parts of the book.

May 2011