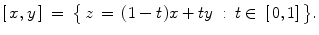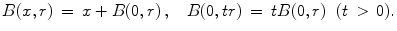The setting is that of a vector space over the real numbers
. There are a dozen or so axioms that define a vector space (the number depends on how they are phrased), bearing upon the existence and the properties of certain operations called addition and scalar multiplication. It is more than probable that the reader is fully aware of these, and we shall say no more on the matter. We turn instead to the central idea of this chapter.
A norm on the vector space X corresponds to a reasonable way to measure the size of an element, one that is consistent with the vector operations. Given a point x X , the norm of x is a nonnegative number, designated x . We also write x X at times, if there is a need to distinguish this norm from others. In order to be a norm, the mapping x x must possess the following properties:
x 0 x X ; x =0 if and only if x =0 ( positive definiteness );
x + y x + y x , y X ( the triangle inequality );
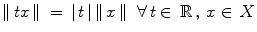
( positive homogeneity ).
Once it has been equipped with a norm, the vector space X , or, more precisely perhaps, the pair ( X ,), is referred to as a normed space .
We have implied that vector spaces and topology are to meet in this chapter; where, then, is the topology? The answer lies in the fact that a norm induces a metric on X in a natural way: the distance d between x and y is d ( x , y )= x y . Thus, a normed space is endowed with a metric topology, one (and this is a crucial point) which is compatible with the vector space operations.
Some notation.
The closed and open balls in X are (respectively) the sets of the form
where the radius r is a positive number. We sometimes write B or B X for the closed unit ball B (0,1), and
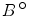
for the open unit ball
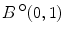
. A subset of X is bounded if there is a ball that contains it.
If A and C are subsets of X and t is a scalar (that is, an element of
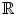
), the sets A + C and tA are given by
(Warning: A + A is different from 2 A in general.) Thus, we have
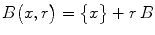
. We may even ask the reader to tolerate the notation B ( x , r )= x + r B . The closure of A is denoted cl A or
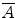
, while its interior is written int A or
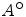
.
Given two points x and y in X , the closed interval (or segment) [ x , y ] is defined as follows:
When t is restricted to (0,1) in the definition, we obtain the open interval ( x , y ). The half-open intervals [ x , y ) and ( x , y ] are defined in the evident way, by allowing t to vary in [0,1) and (0,1] respectively.
The compatibility between the vector space and its norm topology manifests itself by the fact that if U is an open subset of X , then so is its translate x + U and its scalar multiple tU (if t 0). This follows from the fact that balls, which generate the underlying metric topology, cooperate most courteously with the operations of translation and dilation:
It follows from this, for example, that we have int( tA )= t int A when t 0, and that a sequence x i converges to a limit x if and only if the difference x i x converges to 0. There are topologies on X that do not respect the vector operations in this way, but they are of no interest to us. We shall have good reasons later on to introduce certain topologies on X that differ from that of the norm; they too, however, will be compatible with the vector operations.
A vector space always admits a norm. To see why this is so, recall the well-known consequence of Zorns lemma which asserts that any vector space has a basis { e }, in the sense of linear algebra. This means that any x has a unique representation x = x e , where all but a finite number of the coefficients x are 0. The reader will verify without difficulty that x := | x | defines a norm on X . In practice, however, there arises the matter of choosing a good norm when a space presents multiple possibilities.
Sometimes a good norm (or any norm) is hard to find. An example of this: the space of all continuous functions f from
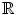












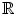 . The central idea of this chapter is that of a norm . It is studied in detail, along with the attendant concept of linear operators. The dual space is introduced. The chapter ends with a presentation of derivates, directional derivatives, tangent and normal vectors. These constructs, which allow one to reduce nonlinear situations to linear ones, will play a central role in later developments.
. The central idea of this chapter is that of a norm . It is studied in detail, along with the attendant concept of linear operators. The dual space is introduced. The chapter ends with a presentation of derivates, directional derivatives, tangent and normal vectors. These constructs, which allow one to reduce nonlinear situations to linear ones, will play a central role in later developments.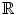 . There are a dozen or so axioms that define a vector space (the number depends on how they are phrased), bearing upon the existence and the properties of certain operations called addition and scalar multiplication. It is more than probable that the reader is fully aware of these, and we shall say no more on the matter. We turn instead to the central idea of this chapter.
. There are a dozen or so axioms that define a vector space (the number depends on how they are phrased), bearing upon the existence and the properties of certain operations called addition and scalar multiplication. It is more than probable that the reader is fully aware of these, and we shall say no more on the matter. We turn instead to the central idea of this chapter.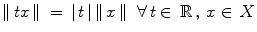 ( positive homogeneity ).
( positive homogeneity ).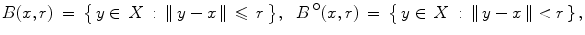
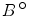 for the open unit ball
for the open unit ball 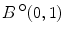 . A subset of X is bounded if there is a ball that contains it.
. A subset of X is bounded if there is a ball that contains it. ), the sets A + C and tA are given by
), the sets A + C and tA are given by 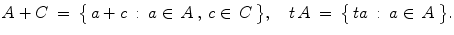
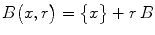 . We may even ask the reader to tolerate the notation B ( x , r )= x + r B . The closure of A is denoted cl A or
. We may even ask the reader to tolerate the notation B ( x , r )= x + r B . The closure of A is denoted cl A or 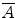 , while its interior is written int A or
, while its interior is written int A or 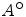 .
.