Peter D. Lax - Functional Analysis

PURE AND APPLIED MATHEMATICS

A Wiley-Interscience Series of Texts, Monographs, and Tracts

Founded by RICHARD COURANT
Editors: MYRON B. ALLEN III, DAVID A. COX, PETER LAX
Editors Emeriti: PETER HILTON, HARRY HOCHSTADT, JOHN TOLAND

A complete list of the titles in this series appears at the end of this volume.

Copyright 2002 by John Wiley & Sons, Inc. All rights reserved.

Published simultaneously in Canada.

No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4744. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 605 Third Avenue, New York, NY 10158-0012, (212) 850-6011, fax (212) 850-6008, E-mail: .

For ordering and customer service, call 1-800-CALL-WILEY.

Library of Congress Cataloging-in-Publication Data

Lax, Peter D.

Functional analysis / Peter D. Lax.
p. cm.
Includes bibliographical references and index.
ISBN 0-471-55604-1 (cloth : alk. paper)
1. Functional analysis. I. Title.

QA320.L345 2002

515dc21 2001046547

20 19 18

CONTENTS

FOREWORD

This book grew out of a course of lectures on functional analysis taught over many years to second-year graduate students at the Courant Institute of New York University. It is a graduate text, not a treatise or a monograph. Most of the chapters are short, for it is easier to digest material in small chunks. Not all topics can be presented briefly, so some of the chapters are longer. Theorems and lemmas, as well as equations, are numbered consecutively in each chapter.

The first 23 chapters make only a modest technical demand on the reader; this material would serve very well as text for an introductory graduate course on functional analysis. The rest of the material is well suited as text for a more advanced graduate course on functional analysis in general, or on Hilbert space in particular.

When I was a student, the only text on functional analysis was Banachs original classic, written in 1932; Hilles book appeared in time to serve as my graduation present. For Hilbert space there was Stones Colloquium publication, also from 1932, and Sz.-Nagys Ergebnisse volume. Since then, our cup hath run over; first came Riesz and Sz.-Nagy, then Dunford and Schwartz, Yosida, later Reed and Simon, and Rudin. For Hilbert space, there was Halmoss elegant slender volume, and Achiezer and Glazman, all of which I read with pleasure and profit. Many, many more good texts have appeared since. Yet I believe that my book offers something new: the order in which the material is arranged, the interspersing of chapters on theory with chapters on applications, so that cold abstractions are made flesh and blood, and the inclusion of a very rich fare of mathematical problems that can be clarified and solved from the functional analytic point of view.

In choosing topics I heeded the warning of my teacher Friedrichs: It is easy to write a book if you are willing to put into it everything you know about the subject. I present the basic structure of the subject, and those more advanced topics that loom large in the body of mathematics. Among these are the spectral resolution and spectral representation of self-adjoint operators, the theory of compact operators, the Krein-Milman theorem, Gelfands theory of commutative Banach algebras, invariant subspaces, strongly continuous one-parameter semigroups. I discuss the index of operators, so important in calculating topological invariants; the celebrated trace formula of Lidskii, a powerful tool in analysis; the Fredholm determinant and its generalizations, rising again after almost a hundred years of hibernation; and scattering theory, another gift from physics to mathematics. I have also included some (but not all) special topics close to my heart.

What has been omitted? All of nonlinear functional analysis, for which I recommend the four-volume treatise by Zeidler. Operator algebras, except for Gelfands theory of commutative Banach algebras. I slight the geometric theory of Banach spaces; happily a handbook on this subject, edited by Bill Johnson and Joram Lindenstrauss is about to be published by North Holland.

What are the prerequisites? What every second-year graduate student-and many undergraduatesknows:

• Naive set theory. Denumerable sets, the continuum, Zorns lemma.
• Linear algebra. The alternative for linear maps, trace and determinant of a matrix, the spectral theory of general and symmetric matrices, functions of a matrix.
• Point set topology. Complete metric spaces, the Baire category principle, Hausdorff spaces, compact sets, Tychonovs theorem.
• Basic theory of functions of a complex variable.
• Real variables. The Arzela-Ascoli theorem, the Lebesgue decomposition of measures on 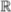, Borel measure on compact spaces.

It is an accident of history that measure theory was invented before functional analysis. The usual presentations of measure theory fail to take advantage of the concepts and constructions of functional analysis. In an appendix on the Riesz-Kakutani representation theorem I show how to use the tools of functional analysis in measure theory. Another appendix summarizes the basic facts of Laurent Schwartzs theory of distributions.

Many of the applications are to problems of partial differential equations. Here a nodding aquaintance with the Laplace and the wave equation would help, although an alert uninformed reader could pick up some of the basic results from these pages.

Like most mathematicians, I am no historian. Yet I have included historical remarks in some of the chapters, mainly where I had some firsthand knowledge, or where conventional history has been blatantly silent concerning the tragic fate of many of the founding fathers of functional analysis during the European horrors of the 1930s and 1940s.

I am indebted to many. I learned the rudiments of functional analysis, and how to apply them, from my teacher Friedrichs. Subsequently my views were shaped by the work of Tosio Kato, who has brought the power of functional analysis to bear on an astonishing range of problems. My happy and long collaboration with Ralph Phillips has led to some unusual uses of functional analysis. r learned much from Israel Gohberg, especially about the index of Toeplitz operators, from Bill Johnson about the fine points of the geometry of Banach spaces, and from Bob Phelps about Choquets theorem. I thank Reuben Hersh and Louise Raphael for their critique of the appendix on distributions, and Jerry Goldstein for his expert comments on the material on semigroups and scattering theory. To all of them, as well as to Gabor Francsics, my thanks.

Jerry Berkowitz and I alternated teaching functional analysis at the Courant Institute. This would be a better book had he lived and looked the manuscript over critically.

I thank Jeff Rosenbluth and Paul Chernoff for a careful reading of the early chapters, and Keisha Grady for TEXing the manuscript, and cheerfully making subsequent changes and corrections.