Benjamin Steinberg Universitext Representation Theory of Finite Groups An Introductory Approach 10.1007/978-1-4614-0776-8_1 Springer Science+Business Media, LLC 2012
1. Introduction
Abstract
The representation theory of finite groups is a subject going back to the late eighteen hundreds. The pioneers in the subject were G. Frobenius, I. Schur, and W. Burnside. Modern approaches tend to make heavy use of module theory and the Wedderburn theory of semisimple algebras. But the original approach, which nowadays can be thought of as via discrete Fourier analysis, is much more easily accessible and can be presented, for instance, in an undergraduate course. The aim of this text is to exposit the essential ingredients of the representation theory of finite groups over the complex numbers assuming only knowledge of linear algebra and undergraduate group theory, and perhaps a minimal familiarity with ring theory.
The representation theory of finite groups is a subject going back to the late eighteen hundreds. The pioneers in the subject were G. Frobenius, I. Schur, and W. Burnside. Modern approaches tend to make heavy use of module theory and the Wedderburn theory of semisimple algebras. But the original approach, which nowadays can be thought of as via discrete Fourier analysis, is much more easily accessible and can be presented, for instance, in an undergraduate course. The aim of this text is to exposit the essential ingredients of the representation theory of finite groups over the complex numbers assuming only knowledge of linear algebra and undergraduate group theory, and perhaps a minimal familiarity with ring theory.
The original purpose of representation theory was to serve as a powerful tool for obtaining information about finite groups via the methods of linear algebra, e.g., eigenvalues, inner product spaces, and diagonalization. The first major triumph of representation theory was Burnsides pq -theorem. This theorem states that a non-abelian group of order p a q b with p , q prime cannot be simple, or equivalently, that every finite group of order p a q b with p , q prime is solvable. It was not until much later [2, 14] that purely group theoretic proofs were found. Representation theory went on to play an indispensable role in the classification of finite simple groups.
However, representation theory is much more than just a means to study the structure of finite groups. It is also a fundamental tool with applications to many areas of mathematics and statistics, both pure and applied. For instance, sound compression is very much based on the fast Fourier transform for finite abelian groups. Fourier analysis on finite groups also plays an important role in probability and statistics, especially in the study of random walks on groups, such as card shuffling and diffusion processes [7, 3], and in the analysis of data [7, 8]; random walks are considered in the last chapter of the book. Applications of representation theory to graph theory, and in particular to the construction of expander graphs, can be found in [6]. Some applications along these lines, especially toward the computation of eigenvalues of Cayley graphs, are given in this text.
Benjamin Steinberg Universitext Representation Theory of Finite Groups An Introductory Approach 10.1007/978-1-4614-0776-8_2 Springer Science+Business Media, LLC 2012
2. Review of Linear Algebra
This chapter reviews the linear algebra that we shall assume throughout the book. Proofs of standard results are mostly omitted. The reader can consult a linear algebra text such as [4] for details. In this book all vector spaces considered will be finite dimensional over the field
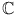
of complex numbers.
2.1 Basic Definitions and Notation
This section introduces some basic notions from linear algebra. We start with some notation, not all of which belongs to linear algebra. Let V and W be vector spaces.
If X is a set of vectors, then
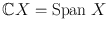
.
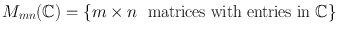
.
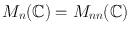
.
Hom( V , W )={ A : V W A { is a linear map}}.
End( V )=Hom( V , V ) (the endomorphism ring of V ).
GL ( V )={ A End( V ) A { is invertible}} (known as the general linear group of V ).
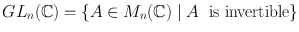
.
The identity matrix/linear transformation is denoted I , or I n if we wish to emphasize the dimension n .
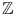
is the ring of integers.
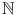
is the set of non-negative integers.
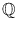
is the field of rational numbers.
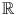
is the field of real numbers.
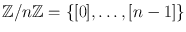
is the ring of integers modulo n .
R denotes the group of units (i.e., invertible elements) of a ring R .
S n is the group of permutations of {1,, n }, i.e., the symmetric group on n letters.
The identity permutation is denoted Id .
Elements of
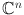



















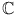 of complex numbers.
of complex numbers.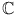 of complex numbers.
of complex numbers.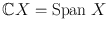 .
.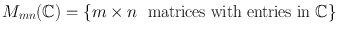 .
.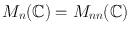 .
.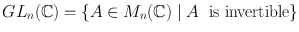 .
.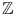 is the ring of integers.
is the ring of integers.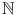 is the set of non-negative integers.
is the set of non-negative integers.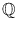 is the field of rational numbers.
is the field of rational numbers.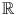 is the field of real numbers.
is the field of real numbers.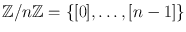 is the ring of integers modulo n .
is the ring of integers modulo n .