Saul Stahl - Introductory Modern Algebra: A Historical Approach

Introductory Modern Algebra

Copyright 2013 by John Wiley & Sons, Inc. All rights reserved.

Published by John Wiley & Sons, Inc., Hoboken, New Jersey. Published simultaneously in Canada.

No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 750-4470, or on the web at www.copyright.com . Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008, or online at http://www.wiley.com/go/permission .

Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representation or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created or extended by sales representatives or written sales materials. The advice and strategies contained herein may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.

For general information on our other products and services please contact our Customer Care Department within the United States at (800) 762-2974, outside the United States at (317) 572-3993 or fax (317) 572-4002.

Wiley also publishes its books in a variety of electronic formats. Some content that appears in print, however, may not be available in electronic formats. For more information about Wiley products, visit our web site at www.wiley.com .

Library of Congress Cataloging-in-Publication Data:

Stahl, Saul.
Introductory modern algebra : a historical approach / Saul Stahl, Department of Mathematics,
University of Kansas. Second edition.
p. cm.
Includes bibliographical references and index.
ISBN 978-0-470-87616-9 (cloth)
1. Algebra, Abstract. I. Title.
QA162.S73 2013
512.02dc23
2013018928

Preface

IT IS COMMON KNOWLEDGE amongst mathematicians that much of modern algebra has its roots in the issue of solvability of equations by radicals. The purpose of this text is to provide the undergraduate mathematics majors and the prospective high school mathematics teachers with a one-semester introduction to modern algebra that keeps this relationship in view at all times.

Most modern algebra texts employ an axiomatic strategy that begins with abstract groups and ends with fields, ignoring the issue of solvability of equations by radicals. By contrast, we follow the paper trail from the Renaissance solution of the cubic equation to Galoiss description of his ideas. In the process, all the important concepts are encountered, each in a well-motivated manner.

One year of calculus provides all the information required for the comprehension of all the topics in this text, which has many distinguishing features:

Historical development. Students would prefer to know the real reasons that underlie the creation of the mathematical structures they encounter. They also enjoy being placed in direct contact with the works of the prime movers of mathematics. This text tries to bring them as close to the source as possible.

Finite groups and fields are rooted in some specific investigations of Lagrange, Gauss, Cauchy, Abel, and Galois regarding the solvability of equations by radicals, This text makes these connections explicit. Gausss proof of the constructibility of the regular 17-sided polygon is incorporated into the development, and the argument given is merely a paraphrase of that which appears in the Disquisitiones. Similarly, the proof of Theorem 8.10 is just a reorganization of that given by Abel in his paper on the quintic equation. The construction of Galois fields is accomplished in the form of a commentary on the opening pages of Galoiss paper On the Theory of Numbers which are quoted verbatim in the text. Several important documents are also included as appendices. A considerable amount of historical discussion is integrated into the development of the subject matter.

Cohesive organization. The historical development of the material allows for very little flexibility. Each chapter elucidates some of the preceding material and motivates ideas that come later. The advantage of this approach is the same as that of good motivation in general: it aids comprehension by providing the students with a framework in which to fit the various concepts they encounter. A one semester course can be constructed on the basis of Sections 1.1, 2.15, 3.12. 4.12, 5.12, 6.13, 7.13, 8.14, 9.15, & 10.1.

illustrates the authors perception of the evolution of abstract group theory (ignoring all the geometric and much of the number-theoretic contributions). The number in the right of each box denotes the chapter in which this topic is discussed. Solid arrows correspond to connections that are treated in some depth whereas those that are displayed by dashed arrows are touched on only informally.

The genesis of the theory of finite groups.

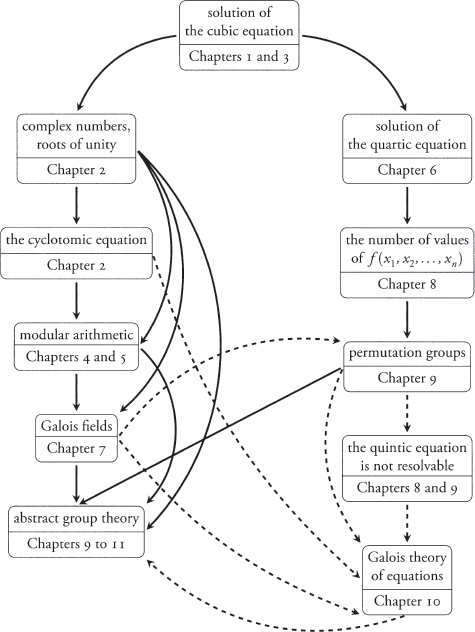
Chapters 1 to 3 are dedicated to the formalization of the notion of solvability by radicals. Gausss proof of the constructibility of the regular 17-sided polygon is the capstone theorem of this part of the course. Field theory is developed in Chapters 4 to 7. The Primitive Element Theorem of Section 7.3 serves as a watershed: it unifies many of the important concepts that precede it and motivates the notion of cyclicity that comes later. Group theory is developed in Chapters 8 to 10. This begins with an explanation of the relevance of permutations to solvability by radicals, goes on to the discussion of permutation groups and abstract groups, and concludes with the description of quotient groups. Chapter 11 is meant to acquaint the students with some of the standard tools of elementary group theory.

Exercises. Each section is followed by its own set of exercises. These range from the routine to the challenging. Each chapter has an additional set of easy review exercises added to remind the students of the chapters main points. There are over 1,000 of these end-of-section and chapter review exercises. The answers to selected odd exercises appear at the end of the book. Most chapters are also accompanied by a collection of supplementary computer and/or mathematical projects. Some of the latter involve open questions.

Additional pedagogy. Each chapter begins with an introduction and concludes with a summary. The purposes of both the introduction and the summary are to provide the student with an overview of the chapter, and sometimes to comment on its relationship to the previous chapters. The examples are integrated into the exposition and they are highlighted by a notation in the margin. Each chapters new terms are listed, together with the pages on which they are defined, following that chapters summary.