Whether you are looking to learn about pre-algebra and algebra for the first-time or you would like to review your math skills, this book will be a great choice. Starting with basic exercises with integers and rational numbers, youll learn about variables, algebraic expressions, and algebraic sentences. You also will learn to solve two-step and multistep equations, as well as inequalities.
Pre-Algebra and Algebra Smarts! provides clear lessons with many easy-to-learn techniques and plenty of examples.
About the Authors Lucille Caron and Philip M. St.
Jacques are New Jersey public school educators. They have collaborated on various educational math projects, including editing, test writing, and text book committee work. 
If you were to look up the meaning of the word
mathematics, you would find that it is the study of numbers, quantities, and shapes, and how they are related to each other. Mathematics is very important to all world cultures, including our world of work. The following are just some of the ways in which studying math will help you: You will know how much money you are spending at the store. You will know if the cashier has given you enough change.
You will know how to use measurements to build things. Your science classes will be easier and more interesting. You will understand music on a whole new level. You will be empowered to qualify for and land a rewarding job. Algebra is a branch of mathematics. It uses the same basic operations that you have learned: addition, subtraction, multiplication, and division.
However, algebra deals with properties of numbers using symbols. People need to know algebra to find out if they received the correct change at the store. Engineers use algebra to set the timing of different traffic lights on a street or to design the shape of a sports ball. This book has been written so that you can learn about pre-algebra at your own speed. It will help you get prepared for your future study of algebra. 
Algebra helps us understand mathematics in a general way.

Algebra helps us understand mathematics in a general way.
In algebra, letters represent numbersincluding whole numbers, integers, and rational numbers. Mathematical rules, though, still apply. So that you can see why algebra works and how it applies to real life, lets review the different kinds of numbers, their operations, and the properties of their operations. Whole Numbers and Integers Whole numbers consist of the counting numbers and zero. Whole Numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, We can represent whole numbers on a number line.  All the whole numbers, except for zero, are called positive integers.
All the whole numbers, except for zero, are called positive integers.
Zero is an integer, but it is neither positive nor negative. We can represent positive integers on the number line by placing a positive sign (+) before each whole number. A positive sign indicates that the number is larger than zero. 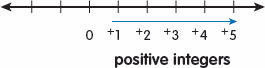 Numbers smaller than zero are called negative integers. We can represent negative integers on the number line by placing a negative sign () before each number. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four.
Numbers smaller than zero are called negative integers. We can represent negative integers on the number line by placing a negative sign () before each number. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four.
The symbol is placed on the upper left of the numeral. The negative and positive signs are raised to distinguish them from the signs for the operation of addition (plus, +) and subtraction (minus, ). Four units to the left of zero on a number line are shown. 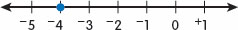 A +4 is read, Positive four. The number 4 is a whole number. We can read the number 4 as four or positive four.
A +4 is read, Positive four. The number 4 is a whole number. We can read the number 4 as four or positive four.
If the positive sign (+) is not written before a number, the number is understood to be positive. Opposites Opposites are pairs of numbers that are the same distance away from zero, but on opposite sides. Every number has only one opposite. Look at the number line. The opposite of 2 is +2.  Notice that 2 and +2 are the same distance away from zero.
Notice that 2 and +2 are the same distance away from zero.
The 2 is two units to the left of zero while the +2 is two units to the right of zero. These pairs of numbers are opposites.
Numbers greater than zero are
positive and are to the right of zero on a number line. Numbers less than zero are
negative and are to the left of zero on a number line.
A rational number is a number that can be written as a fraction. They include positive and negative whole numbers, mixed numerals, repeating decimals, and terminating decimals.
Zero is also a rational number. Some examples of rational numbers are:  Number Line Positive rational numbers are represented by a positive sign (+). A positive sign indicates that the number is greater than zero.
Number Line Positive rational numbers are represented by a positive sign (+). A positive sign indicates that the number is greater than zero. 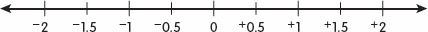 Negative rational numbers are represented by a negative sign (). A negative sign indicates that the number is smaller than zero. +0.5 is 0.5 units to the right of zero. 0.5 is 0.5 units to the left of zero. 0.5 is 0.5 units to the left of zero.
Negative rational numbers are represented by a negative sign (). A negative sign indicates that the number is smaller than zero. +0.5 is 0.5 units to the right of zero. 0.5 is 0.5 units to the left of zero. 0.5 is 0.5 units to the left of zero.
These two points are opposites because they are the same distance from zero but on opposite sides of zero.
rational numberA number that can be written as a fraction. Rational numbers have opposites just like integers do. Writing a Whole Number as a Rational Number To write a whole number as a rational number, place the whole number over one. For example, to write 6 as a rational number, place the whole number over one.
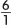 Writing a Mixed Numeral as a Rational Number
Writing a Mixed Numeral as a Rational Number
+ Rational Concentration Play rational concentration with a family member.
Make twenty cards with examples of positive and negative rational numbers. Use some of the examples below: 













 All the whole numbers, except for zero, are called positive integers.
All the whole numbers, except for zero, are called positive integers. Numbers smaller than zero are called negative integers. We can represent negative integers on the number line by placing a negative sign () before each number. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four.
Numbers smaller than zero are called negative integers. We can represent negative integers on the number line by placing a negative sign () before each number. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four. Integers are the counting numbers, the negative of these, and zero: 3, 2, 1, 0, 1, 2, 3, Reading and Writing Integers A 4 is read, Negative four.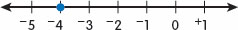 A +4 is read, Positive four. The number 4 is a whole number. We can read the number 4 as four or positive four.
A +4 is read, Positive four. The number 4 is a whole number. We can read the number 4 as four or positive four. Notice that 2 and +2 are the same distance away from zero.
Notice that 2 and +2 are the same distance away from zero. Number Line Positive rational numbers are represented by a positive sign (+). A positive sign indicates that the number is greater than zero.
Number Line Positive rational numbers are represented by a positive sign (+). A positive sign indicates that the number is greater than zero. 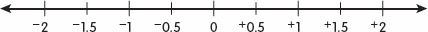 Negative rational numbers are represented by a negative sign (). A negative sign indicates that the number is smaller than zero. +0.5 is 0.5 units to the right of zero. 0.5 is 0.5 units to the left of zero. 0.5 is 0.5 units to the left of zero.
Negative rational numbers are represented by a negative sign (). A negative sign indicates that the number is smaller than zero. +0.5 is 0.5 units to the right of zero. 0.5 is 0.5 units to the left of zero. 0.5 is 0.5 units to the left of zero.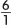 Writing a Mixed Numeral as a Rational Number
Writing a Mixed Numeral as a Rational Number + Rational Concentration Play rational concentration with a family member.
+ Rational Concentration Play rational concentration with a family member. 