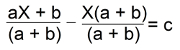THE EASIEST WAY TO UNDERSTAND ALGEBRA Roy Richard Sawyer
Copyright 2017 by Roy Richard Sawyer - All rights reserved
INTRODUCTION There is a voice inside you that always says," You can't do that. Leave it." This is not true, but you believe this voice because you get some benefit from accepting the advice. You get a good excuse to slip away from your work. You can go out with friends, watch TV, or do whatever you want. However, you cannot feel genuine pleasure from your entertainment because there is a part of you who wants to be proud of your achievements. This voice tells to "Keep trying! You can do that! You are smart." Believe in what this voice is saying! This tutorial will show you a way of thinking that will help you to understand math.
This tutorial is for anyone who wants to feel comfortable using a mathematical formula; who wants to comprehend the beauty of algebraic expressions. Did you ever feel frustration looking at your math text book? Forget it! Fall in love with math! 1. HOW TO SOLVE THE EQUATIONS Math is a very enjoyable field of activity. Having just a pen and a piece of paper you can invent whatever you want. You can wander around the paper with numbers and symbols caring about just one thing: equality should be equality, nothing more. Let us imagine that you are the first great mathematician.
People are only familiar with arithmetic: how to add, subtract, multiply and divide. In school, they study boring things such as these expressions: 2 + 3 = 5 or 7 - 4 = 3 You are the first who suspects there is a way to express a common idea of the equations written above. First you write: a + b = c or c - a = b. Now you have discovered common rules that can help people to solve any equation. To verify the discovery, you have to perform experiments with numbers. 4 + 8 + 3 = 12 What did you get? 15 = 12 This is incorrect! How can you fix your equation? You must add the same number to the right side of the equation. 4 + 8 + = 12 + . 4 + 8 + = 12 + .
What did you get? 15 = 15 You discovered the first rule for equations. This rule says: "If you add the same number to the left side and to the right side of an equation, this equation will still be true." To express this rule in a common way you can write: If a + b = c then a + b + n = C + n where a, b, c, n equal any numbers. Are you a genius? Of course, you are! Go ahead. Let us try another experiment. What happens if you subtract any number from the left side of an equation? 5+2=7 5+2-5=7 What did you get? 2 = 7 This is incorrect, but you know how to fix your equation. 5 + 2 - = 7 - . 5 + 2 - = 7 - .
Then 2 = 2. Congratulations! You discovered the second rule for equations. This rule says: "If you subtract the same numbers from the left and the right side of an equation this equation will still be true." Or you can write: if a + b = c then a + b - n = c - n where a, b, c, n equal any numbers. What other kind of experiments can you do? You can multiply one side of an equation by some number. Let's write an equation: 5 - 1 = 4 What happens, if you multiply the left side of the equation by 7? (5 - 1)7 = 4 then 28 = 4 This is not true. (5 -1)= 4 x . (5 -1)= 4 x .
Then 28 = 28 You discovered one more rule for equations. The third rule says: " If you multiply the left and the right side of an equation by the same number, this equation will still be true." if a - b = c then (a - b) n = (c) n One more question. What happens if you divide one half of an equation by any number? 4 + 6 = 10 (4 + 6)/2 = 10 then 5 = 10. You can ask yourself, "How many times will I make the same mistake?" But you have the knowledge to fix the problem. You must divide both sides of the equation by the same number. (4 + 6): = 10: then 5 = 5 You discovered the fourth rule for equations.
This rule says: "If you divide the left and the right side of an equation by the same number the equation will still be true." So, you can write: if a + b = c then (a + b)/ n = c/ n Where a, b, c, are any numbers, but n does not equal to 0 because you can't divide numbers by 0. People will ask you, "What kind of benefit can you get from these rules?" Your response will be, "You can use these rules to solve any equation." Let us write an equation where one number is unknown. X - 3 = 11 How can we solve this equation? Try to apply the first rule: If you add the same number to the left and the right side of an equation, this equation will be true. For our equation, it is convenient to add 3 to both sides of the equation. X - 3 + = 11 + Since -3 + 3 = 0 Then X = 11 + 3 So, X=14 Let us try to solve an equation where all numbers are represented by lepers. X - b = c Apply the first rule to solve this equation X - b + b = c + b Since, -b + b = 0, then X = c + b.
To solve the equation X + b = c we can apply the second rule. If X + b = c then X + b - b = c - b X = c - b. The next example is X + 7 = 15 then X + 7 - = 15 - and X = 8 Do not proceed until you perform some exercises to become comfortable using the first few rules of equations. Practice 1. Solving the equations. Solve for X: You can find the answers in appendix 1.
If your answer is wrong try again. If you can't get the right answer read the solution in appendix 2. Let's solve the equation 4X - 5 = 15 You can apply the first rule. 4X - 5 + = 15 + then 4X = 20. How can you find X? You can apply the fourth rule. 4X / = 20 / , then X = 5. 4X / = 20 / , then X = 5.
To solve equation aX - b = c Apply the first rule. aX - b + b = c + b , then aX = c + b Now apply the fourth rule. If aX = c + b, then aX / a = (c + b) / a and X = (c + b)/ a Do not read any more until you perform some exercises. Practice 2. Solving the equations. Solve for X: Answers are in appendix 1.
Solutions are in appendix 2. If you have such an equation to solve: X/a - 5 = 6 Then apply the first rule: X/a - 5 + = 6 + X/a = 6 + 5 X/a = 11 Then apply the third rule. X/a * a = 11 * a X = 11a Let's solve the equation: 2X - 4b = 2bc Apply the first rule: 2X - 4b + 4b = 2bc + 4b , then 2X = 2bc + 4b Apply the third rule: 2X/ = (2bc + 4b) / You should know how to divide a binomial by a monomial. If you have forgotten it, you could find the rule by yourself. Can you write? (2bc+ 4b)/ = 2bc/ + 4b/. Yes, you can.
Let' us check. Suppose, c = 2 and b = 3. To divide a binomial by 2, try to divide each monomial by 2 2*3*2/ + 4*3/ = 12 Now try to solve the binomial first and then divide by 2 (2*3*2 + 4*3)/ then 24/ = 12 We got the same answer. It means that (a+ b)/ = a/ + b/. We discovered a rule: To divide a binomial by a number, divide each monomial inside the binomial by that number. 2X = 2bc + 4b. 2X = 2bc + 4b.
Then 2X / = 2bc / + 4b / Then X = bc + 2b You can factor out b and get X = b(c + 2) Whenever you don't know the rule, you can put any numbers in place of the letters and check equality. Discover rules by yourself. Let us solve a more complicated equation: 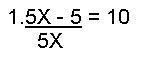 Multiply both sides of the equation by 5X.
Multiply both sides of the equation by 5X. 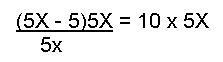 5X - 5 = 50X Use the 2nd rule, subtract 5X from both sides: 5X - 5 - 5X = 50X - 5X or 45X = - 5 Divide both sides by 45
5X - 5 = 50X Use the 2nd rule, subtract 5X from both sides: 5X - 5 - 5X = 50X - 5X or 45X = - 5 Divide both sides by 45 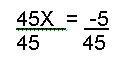 X = - 1/9 The next equation:
X = - 1/9 The next equation: 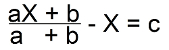 Find the common denominator:
Find the common denominator: 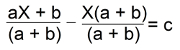
Next page










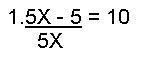 Multiply both sides of the equation by 5X.
Multiply both sides of the equation by 5X. 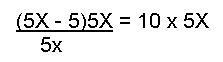 5X - 5 = 50X Use the 2nd rule, subtract 5X from both sides: 5X - 5 - 5X = 50X - 5X or 45X = - 5 Divide both sides by 45
5X - 5 = 50X Use the 2nd rule, subtract 5X from both sides: 5X - 5 - 5X = 50X - 5X or 45X = - 5 Divide both sides by 45 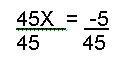 X = - 1/9 The next equation:
X = - 1/9 The next equation: 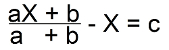 Find the common denominator:
Find the common denominator: