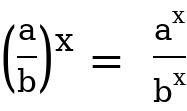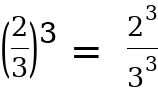Samuel Ade - Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems.
Here you can read online Samuel Ade - Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems. full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems.
- Author:
- Genre:
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems.: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems." wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
100 fully solved problems that explained everything you need to know to independently master algebra and indices is a self teaching workbook that solely solve problems relating to Algebra and indices to help people master this aspect of mathematics without confusion.
This workbook contains solution to problems on the following aspect of algebraic indices;
- Linear equations
- Solving Quadratic expressions
- Exponential equations
- Simultaneous Equations.
- Rational Equations
- Simplification of simple and complex indices problem.
Save yourself the feelings of Mathematics is difficult. Grab your copy of this workbook solution now, as it solve problems ranging from simple to complex.
Samuel Ade: author's other books
Who wrote Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems.? Find out the surname, the name of the author of the book and a list of all author's works by series.
Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems. — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems." online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
- For teachers: He/She reproduce any part for his/her student for teaching practice.
- For parents: He/She reproduce any part of this workbook for his/her children for home practice.
Chapter one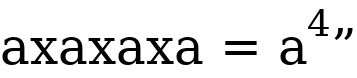A simple way to understand this is shown below. " 
From the example above, 
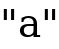is referred to as base, while the number is referred to as power, index, or exponent. Note: For a better understanding of some solutions to some problems, we have to consider the fundamental laws of indices, which will be analyzed below. The following laws will help your understanding to solve any question in indices. 
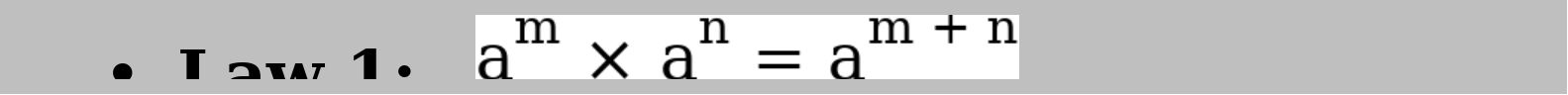This may be referred to as the law of power addition of indices. You can also have ; 
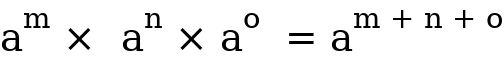(irrespective of the numbers of indices entity you are multiplying above).
For example Given that; x = 
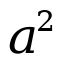and y= 
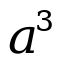, find x 
y. Solution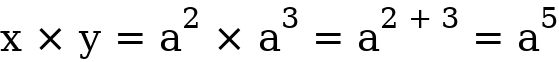 
This can equal be;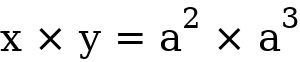 
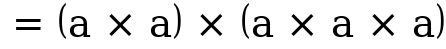
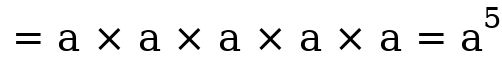But using the law of indices will make the solution easier and faster. For rule 1 to be valid, the bases of both entities must be the same. 
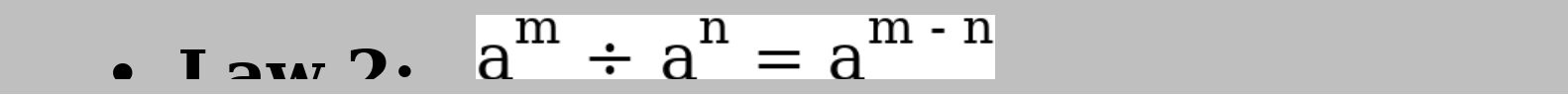For example Given that; x = 
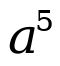and y= , find x 
y. Solution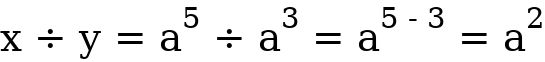 
This can equally be;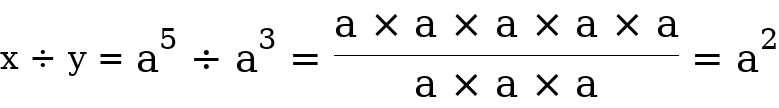 
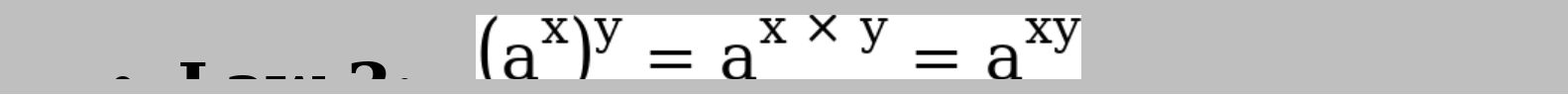For example: 
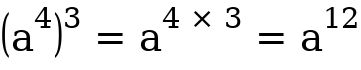This can equally be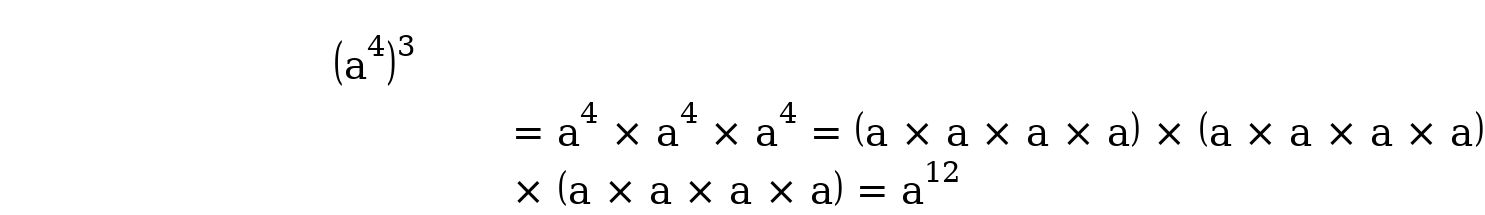 
This is the law of zero index. How do I arrive at this? For example;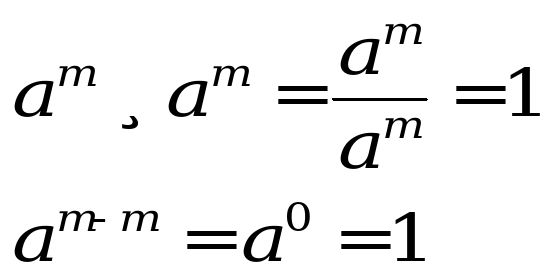 
This is a law of Negative index.
We can still have an example to be, 
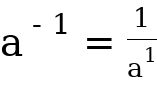Just note that any time you have a Base having a negative index, it is equivalent to the inverse of that base and index, excluding the negative sign. 
This is also known as the law of the fractional index. Given an example of,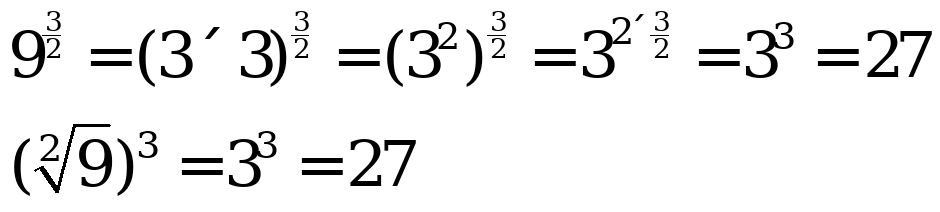 
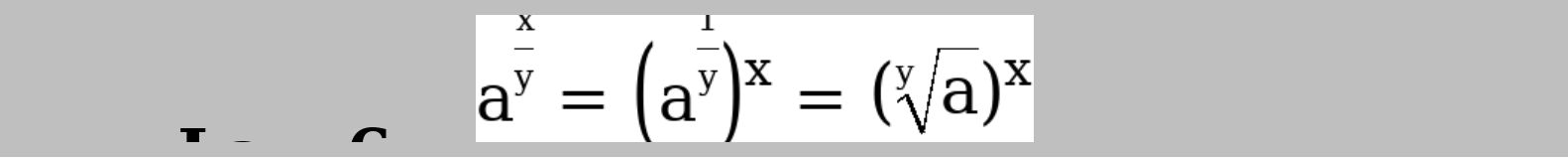For example: 
= 
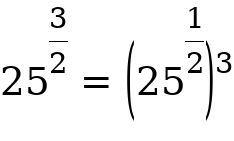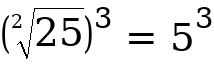= 125 Note the following cases: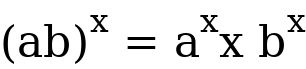
= 
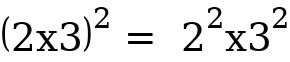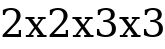= 36 
Font size:
Interval:
Bookmark:
Similar books «Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems.»
Look at similar books to Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems.. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Algebraic Indices: 100 Fully solved problems that explained all you need to know to perfectly understand, improve and independently master Algebra and Indices problems. and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.