45 ADDING/SUBTRACTING REAL NUMBERS ALGEBRA WORKBOOK  PROBLEMS WITH ANSWERS
PROBLEMS WITH ANSWERS  Najwa Hirn
Najwa Hirn
45 ADDING/SUBTRACTING REAL NUMBERS ALGEBRA ADDING/SUBTRACTING REAL NUMBERS PRACTICE PROBLEMS WITH ANSWER KEY AND STEP BY STEP SOLUTIONS Copyright 2019 N. Hirn All rights reserved. Teachers and/or parents who purchase this workbook may make photocopies of the worksheets and solution sheet to use for instructional purposes only. Reproducing this material for commercial purposes is not permitted. HOW TO USE THIS WORKBOOK The study of Mathematics requires understanding of the concepts taught as well as practicing what is learned. It is advisable to practice mathematical problems using pencil and paper to allow the student to follow their train of thoughts as they write each step for the solutions.
This workbook provides 45 problems that require the knowledge and use of the ADDITION AND SUBTRACTION OF REAL NUMBERS rules. These rules are summarized in the next section as a refresher for students. When working out each problem, it is important to learn, understand and apply the rules of ADDITION AND SUBTRACTION OF REAL NUMBERS in order to evaluate the mathematical expressions correctly. The workbook is divided into four sections:
- The first section includes an explanation of the rules that are needed to solve the Order of Operations Problems.
- The second section includes the problems that need solving. The student should use a pencil and paper to copy each problem from the ebook and attempt to solve it independently.
- The third section is the answer key.
- The fourth section includes detailed solutions for each problem explaining the steps involved in reaching the answer.
Hints are provided when a problem requires the use of concepts that are not part of this workbook. Students should be familiar with some of these concepts.
In order to succeed the student should master the material in this section and practice solving each problem. Have fun as you practice and learn how to ADD AND SUBTRACT REAL NUMBERS. RULES FOR ADDING AND SUBTRACTING REAL NUMBERS When working on a mathematical expression it is important to understand how to evaluate each expression in order to obtain the correct answer. In order to learn about Adding and Subtracting Real numbers, it is important to first understand the following terms:
- Number Line
- Real Numbers
- Absolute value
- Opposite numbers
- Terms for Addition and Subtraction
This knowledge can then be used when learning to evaluate the rules associated with Adding and Subtracting Real numbers and how to use them to solve a problem. Explanation Number Line: A Number Line is a straight line that is drawn and labeled with tick marks. A point is labeled somewhere in the middle of the line.
The exact location of is not important as long as it appears somewhere along the middle of the line. This point is called the Origin and it separates the line to a positive side and a negative side. Tick marks are drawn in both direction of at equally spaced distances. The positive side of the number line is to the right of . The numbers to the right of are positive. They increase in value from left to right.
Therefore, moving to the right will mean moving in the positive direction. The numbers to the left of are negative. They decrease in value from right to left. Therefore, moving to the left will mean moving in the negative direction. The following graph illustrates the explanation above: 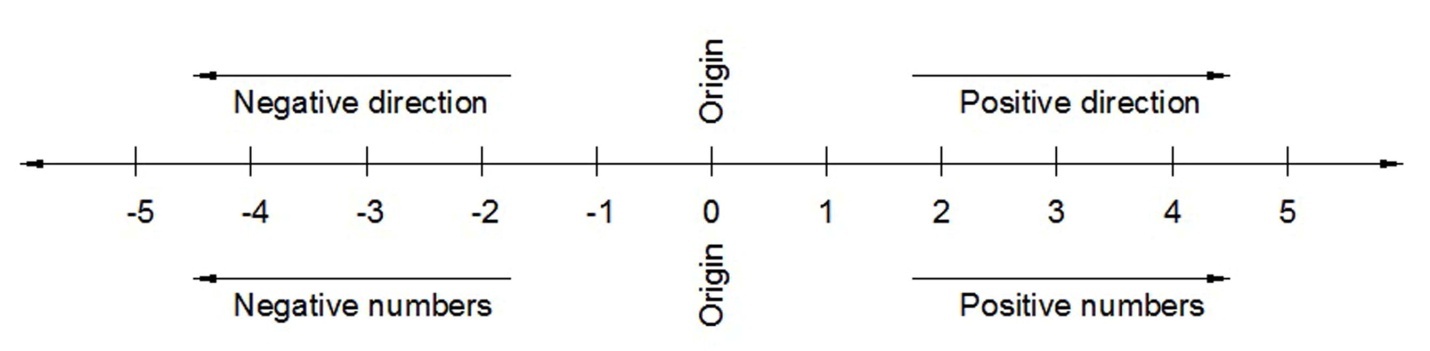 Hint: When comparing two numbers on the number line, the number on the left is always smaller than the number on the right. Real Numbers: Numbers that can be represented with a point on the number line are called Real Numbers.
Hint: When comparing two numbers on the number line, the number on the left is always smaller than the number on the right. Real Numbers: Numbers that can be represented with a point on the number line are called Real Numbers.
They include whole numbers, fractions, decimals and others. Absolute Value: When a number is placed on the Number Line it will have a direction from and a distance from . The Absolute Value of a real number is its distance from and is written enclosed within two short vertical lines as follows: | | Hint: An Absolute Value of a number is never negative. It is the distance of that number from without regards to what direction it is from . Example: The Absolute Value of 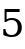 and
and 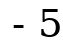 both equal
both equal 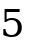 and are written as follows:
and are written as follows: 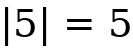
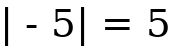 It is just the distance
It is just the distance 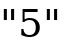 from Opposite Numbers: They are numbers that are the same distance from but are in the opposite direction. Example: The opposite number of
from Opposite Numbers: They are numbers that are the same distance from but are in the opposite direction. Example: The opposite number of 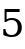 is
is 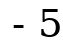 .
.
The opposite number of 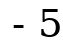 is
is 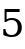 . The above definition of opposite numbers applies to all the numbers on the number line. Terms for Addition and Subtraction Another term for Addition is Sum of. Another term for Subtraction is Difference of. Adding and Subtracting Real Numbers: This workbook will assume that the student is familiar with how to use the Real number line to solve the addition and subtraction of real numbers. This process, which includes plotting a number on the number line then checking its direction then counting units to arrive at the next number, can become very tedious.
. The above definition of opposite numbers applies to all the numbers on the number line. Terms for Addition and Subtraction Another term for Addition is Sum of. Another term for Subtraction is Difference of. Adding and Subtracting Real Numbers: This workbook will assume that the student is familiar with how to use the Real number line to solve the addition and subtraction of real numbers. This process, which includes plotting a number on the number line then checking its direction then counting units to arrive at the next number, can become very tedious.
It is not functional when trying to solve lengthy mathematical problems and therefore will not be addressed in full within working. The rules discussed below are derived from the knowledge of what a Real number line represents; the Absolute value and Opposite of numbers; where to plot numbers on the line and counting their distance from . Rules for Adding and Subtracting Real Numbers: Adding two numbers with the same sign: Add their absolute value and use the common sign. If both numbers are positive the answer will be positive. If both numbers are negative the answer will be negative. Example (1): Adding two positive numbers: 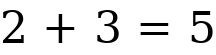 The numbers are added, the result is positive.
The numbers are added, the result is positive.
Example (2): Adding two negative numbers: 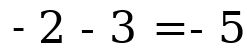 The numbers are added, the result is negative. Hint: When there is no sign in front of a number, that number is always positive. Therefore, the number
The numbers are added, the result is negative. Hint: When there is no sign in front of a number, that number is always positive. Therefore, the number 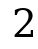
Next page






 PROBLEMS WITH ANSWERS
PROBLEMS WITH ANSWERS  Najwa Hirn
Najwa Hirn Hint: When comparing two numbers on the number line, the number on the left is always smaller than the number on the right. Real Numbers: Numbers that can be represented with a point on the number line are called Real Numbers.
Hint: When comparing two numbers on the number line, the number on the left is always smaller than the number on the right. Real Numbers: Numbers that can be represented with a point on the number line are called Real Numbers. and
and 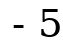 both equal
both equal 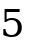 and are written as follows:
and are written as follows: 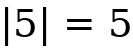
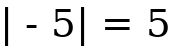 It is just the distance
It is just the distance 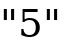 from Opposite Numbers: They are numbers that are the same distance from but are in the opposite direction. Example: The opposite number of
from Opposite Numbers: They are numbers that are the same distance from but are in the opposite direction. Example: The opposite number of 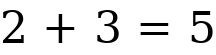 The numbers are added, the result is positive.
The numbers are added, the result is positive.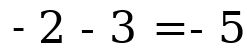 The numbers are added, the result is negative. Hint: When there is no sign in front of a number, that number is always positive. Therefore, the number
The numbers are added, the result is negative. Hint: When there is no sign in front of a number, that number is always positive. Therefore, the number