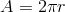To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the FlexBook. CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform.
Copyright 2012 CK-12 Foundation, www.ck12.org
The names "CK-12" and "CK12" and associated logos and the terms "FlexBook" and "FlexBook Platform" (collectively "CK-12 Marks") are trademarks and service marks of CK-12 Foundation and are protected by federal, state, and international laws.
Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link http://www.ck12.org/saythanks (placed in a visible location) in addition to the following terms.
Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution/Non-Commercial/Share Alike 3.0 Unported (CC BY-NC-SA) License (http://creativecommons.org/licenses/by-nc-sa/3.0/), as amended and updated by Creative Commons from time to time (the "CC License"), which is incorporated herein by this reference.
Complete terms can be found at http://www.ck12.org/terms.
ISBN :978-1-935983-77-4
Authors
Andrew McFarland, Mary Fay-Zenk
Say Thanks to Authors
Click http://ck12.org/saythanks
(No Sign in required)
TE Equations and Functions
Overview
Equations and Functions consists of eight lessons that introduce students to the language of algebra.
Suggested Pacing:
Variable Expressions -
Order of Operations -
Patterns and Equations -
Equations and Inequalities -
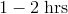
Functions as Rules and Tables -
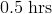
Functions as Graphs -
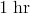
Problem-Solving Plan -
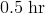
Problem-Solving Strategies: -
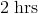 Make a Table; Look for a Pattern
Make a Table; Look for a PatternIf you would like access to the Solution Key FlexBook for even-numbered exercises, the Assessment FlexBook and the Assessment Answers FlexBook please contact us at teacher-requests@ck12.org.
Problem-Solving Strand for Mathematics
The problem-solving strategies presented in this chapter, Make a Table and Look for Patterns , are foundational techniques. Making a Table can help structure a students ability to organize and clarify the data presented and teach the student to communicate more clearly. When teaching Look for a Pattern , ask questions such as:
- Can you identify a pattern in the given examples that would let you extend the data?
- Do you observe any pattern that applies to all the given examples?
- Can you find a relationship or operation(s) that would allow you to predict another term?
Alignment with the NCTM Process Standards
Two promising practices, focused on the communication standards, can be effectively used with these strategies. The first is setting aside a time on a regular basis (i.e. once a week) to have students write about the problem solving they have been doing (COM.2). Present a daily warm-up problem which is well suited to the strategy being learned such as Look for a Pattern . Students work on one problem a day, first individually and then as a group with teacher leadership and summation. Each day the problem is discussed and solved, and many different points of view are shared in the process (COM.1, COM.3). At the end of the week, students are asked to write about any one of the problems they did earlier in the week. This practice pushes students to develop logical thinking skills, to benefit from the classroom work that was shared earlier in the week, and to learn to communicate mathematical ideas clearly (COM.4). It also gives students a choice; they only have to write about one of the problems, and it can be the problem that made the most sense to them. Oftentimes, unfortunately, we do not honor enough what makes sense to students; we expect them only to be able to follow the logic presented to them. We must give them experiences of sense-making as well (RP.1, RP.2).
A second practice is posting student work, such as:
- gallery walks where work in progress can be viewed
- posters that highlight exceptionally well done solutions
- student essays posted on the classroom wall
What matters is that students work is valued and shared (RP.3). If these pieces are large enough to be seen from a distance, this practice helps students to recall various approaches to solving problems (RP.4) and keeps their thinking alive.
- COM.1 - Organize and consolidate their mathematical thinking through communication.
- COM.2 - Communicate their mathematical thinking coherently and clearly to peers, teachers, and others.
- COM.3 - Analyze and evaluate the mathematical thinking and strategies of others.
- COM.4 - Use the language of mathematics to express mathematical ideas precisely.
- RP.1 - Recognize reasoning and proof as fundamental aspects of mathematics.
- RP.2 - Make and investigate mathematical conjectures.
- RP.3 - Develop and evaluate mathematical arguments and proofs.
- RP.4 - Select and use various types of reasoning and methods of proof.
Variable Expressions
Learning Objectives
At the end of this lesson, students will be able to:
- Evaluate algebraic expressions.
- Evaluate algebraic expressions with exponents.
Vocabulary
Terms introduced in this lesson:
algebrageneralizevariablesequationssubstitution (evaluation, plugging-in)valuessolution
Teaching Strategies and Tips
Although the properties of real numbers are not covered until the chapter Real Numbers , some basic working assumptions must be made in this chapter. Addition and multiplication involving negative numbers, for example, will probably not be new to the majority of your students, but it is necessary nonetheless for the completion of the Review problems. A comprehensive assessment prior to the end of the first week of classes is suggested so that you can gauge how much time you will need to cover Equations and Functions and Real Numbers .
Unknowns are used as placeholders in equations like 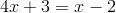 and formulas like
and formulas like 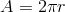
Next page










 Order of Operations -
Order of Operations - 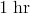 Patterns and Equations -
Patterns and Equations - 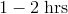 Equations and Inequalities -
Equations and Inequalities - 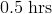 Functions as Graphs -
Functions as Graphs - 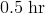 Problem-Solving Strategies: -
Problem-Solving Strategies: -  Make a Table; Look for a Pattern
Make a Table; Look for a Pattern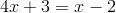 and formulas like
and formulas like