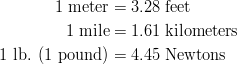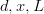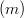CK-12 People's Physics Book Version 3 (with Videos)
To access a customizable version of this book, as well as other interactive content, visit www.ck12.org
No more static textbooks! CK-12 Foundation updates all its FlexBooks on a regular basis. Please visit us at www.ck12.org to access the latest version of this FlexBook and to see previews of coming attractions.
CK-12 Foundation is a non-profit organization with a mission to reduce the cost of textbook materials for the K-12 market both in the U.S. and worldwide. Using an open-content, web-based collaborative model termed the FlexBook. CK-12 intends to pioneer the generation and distribution of high-quality educational content that will serve both as core text as well as provide an adaptive environment for learning, powered through the FlexBook Platform.
Copyright 2011 CK-12 Foundation, www.ck12.org
The names "CK-12" and "CK12" and associated logos and the terms "FlexBook" and "FlexBook Platform" (collectively "CK-12 Marks") are trademarks and service marks of CK-12 Foundation and are protected by federal, state and international laws.
Any form of reproduction of this book in any format or medium, in whole or in sections must include the referral attribution link http://www.ck12.org/saythanks (placed in a visible location) in addition to the following terms.
Except as otherwise noted, all CK-12 Content (including CK-12 Curriculum Material) is made available to Users in accordance with the Creative Commons Attribution/Non-Commercial/Share Alike 3.0 Unported (CC-by-NC-SA) License (http://creativecommons.org/licenses/by-nc-sa/3.0/), as amended and updated by Creative Commons from time to time (the "CC License"), which is incorporated herein by this reference.
Complete terms can be found at http://www.ck12.org/terms.
ISBN :Not Available
Authors
James H. Dann, James Dann
Say Thanks to Authors
Click http://ck12.org/saythanks
(No Sign in required)
Chapter 1: Units and Problem Solving

The Big Idea
Units identify what a specific number refers to. For instance, the number 42 can be used to represent 42 miles, 42 pounds, or 42 elephants! Numbers are mathematical objects, but units give them physical meaning. Keeping track of units can help you avoid mistakes when you work out problems.

http://www.youtube.com/embed/Be2i_9Wu3pk?version=3 Click here to watch the Video
Key Concepts
- Every answer to a physics problem must include units. Even if a problem explicitly asks for a speed in meters per second (m/s), the answer is 5 m/s, not 5.
- When youre not sure how to approach a problem, you can often get insight by considering how to obtain the units of the desired result by combining the units of the given variables. For instance, if you are given a distance (in meters) and a time (in hours), the only way to obtain units of speed (meters/hour) is to divide the distance by the time. This is a simple example of a method called dimensional analysis , which can be used to find equations that govern various physical situations without any knowledge of the phenomena themselves.
- This textbook uses SI units (La Systme International dUnits), the most modern form of the metric system.
- When converting speeds from metric to American units, remember the following rule of thumb: a speed measured in mi/hr is about double the value measured in m/s ( i.e., 10 {m/s} is equal to about 20 MPH). Remember that the speed itself hasnt changed, just our representation of the speed in a certain set of units.
- If a unit is named after a person, it is capitalized. So you write 10 Newtons, or 10 N, but 10 meters, or 10 m.
- Vectors are arrows that represent quantities with direction. In this textbook, vectors will be written in bold. For instance, the force vector will be written as
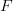 in this textbook. Your teacher will likely use
in this textbook. Your teacher will likely use 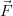 to represent vectors. Dont let this confuse you:
to represent vectors. Dont let this confuse you: 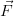 represents the same concept as
represents the same concept as 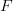 .
.
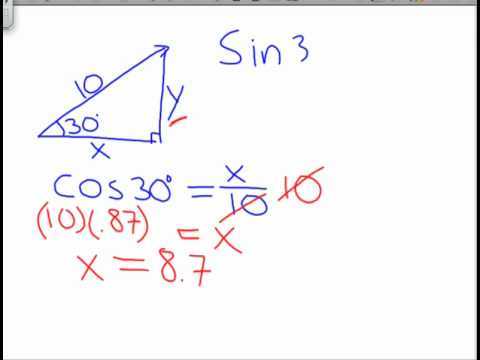
http://www.youtube.com/embed/-DWXF9FgxF8?version=3 Click here to watch the Video

http://www.youtube.com/embed/6ro7uHr07Ts?version=3 Click here to watch the Video
- Vectors can be added together in a simple way. Two vectors can be moved (without changing their directions) to become two legs of a parallelogram. The sum of two vectors is simply the diagonal of the parallelogram:

Key Equations
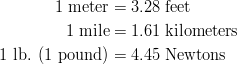
Key Applications
The late great physicist Enrico Fermi used to solve problems by making educated guesses. Say you want to guess timate the number of cans of soda drunk in San Francisco in one year. Youll come pretty close if you guess that there are about 800,000 people in S.F. and that one person drinks on average about 100 cans per year. So, around 80,000,000 cans are consumed every year. Sure, this answer is not exactly right, but it is likely not off by more than a factor of 10 (i.e., an order of magnitude). That is, even though we guessed, were going to be in the ballpark of the right answer. This is often the first step in working out a physics problem.
Table 1.1
| Type of measurement | Commonly used symbols | Fundamental units |
| length or position | 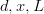 | meters 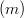 |

















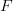 in this textbook. Your teacher will likely use
in this textbook. Your teacher will likely use 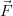 to represent vectors. Dont let this confuse you:
to represent vectors. Dont let this confuse you: 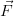 represents the same concept as
represents the same concept as