Britannica Educational Publishing - Algebra

ALGEBRA

Published in 2015 by Britannica Educational Publishing (a trademark of Encyclopdia Britannica, Inc.) in association with The Rosen Publishing Group, Inc.

29 East 21st Street, New York, NY 10010

Copyright 2015 by Encyclopdia Britannica, Inc. Britannica, Encyclopdia Britannica, and the Thistle logo are registered trademarks of Encyclopdia Britannica, Inc. All rights reserved.

Rosen Publishing materials copyright 2015 The Rosen Publishing Group, Inc. All rights reserved

Distributed exclusively by Rosen Publishing.

To see additional Britannica Educational Publishing titles, go to rosenpublishing.com.

First Edition

Britannica Educational Publishing

J. E. Luebering: Director, Core Reference Group

Anthony L. Green: Editor, Comptons by Britannica

Rosen Publishing

Hope Lourie Killcoyne: Executive Editor

Jason Tobin: Editor

Nelson S: Art Director

Michael Moy: Designer

Cindy Reiman: Photography Manager

Karen Huang: Photo Researcher

Library of Congress Cataloging-in-Publication Data

Algebra/edited by Jason Tobin.First edition.

pages cm.(The story of math: core principles of mathematics)

Audience: Grades 7 to 12.

Includes bibliographical references and index.

ISBN 978-1-6227-5522-6 (eBook)

1. AlgebraJuvenile literature. I. Tobin, Jason (Jason Wesley), editor.

QA141.A44 2015

512dc23

2014023206

Photo Credits: Cover and interior pages agsandrew/Shutterstock.com; cover (top), back cover, p. 3 (top) Indivision 07 Grow B/Getty Images; p. 19 Zern Liew/Shutterstock.com.

Contents

A n important branch of mathematics, algebra is studied not only in high school and college, but in the lower grades as well. Although it is dreaded by many students, algebra can be an enjoyable subject. Algebra is practical and as useful as all the other branches of mathematics. For some careers, such as those in engineering and science, knowledge of algebra is indispensable. After reading these chapters, algebra will no longer seem intimidating. In fact, you may be surprised at how often you use it on a daily basis.

It is easy to get hung up on the symbols and complicated story problems for which algebra is famous. However, mathematical concepts that seem so mysterious are often used in regular conversation. The trick is learning how to translate math into English.

For example, suppose an 8-year-old boy asks his father how old he is. Instead of answering the boy directly, the father can attempt an experiment by replying that he is 30 years older than the boy. This is a problem that the son is interested in solving. He can quickly perform the addition and find that his father is 38 years old:

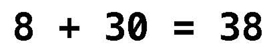
Suppose the boy then asks the age of his mother. The father might at this point present a more challenging problem. For example, the father may answer that if the boy added six years to his mothers age, the result would be equal to the fathers age. The father has thus found an excellent opportunity to help his son understand how an algebraic equation may be made up and solved.

Algebra is less difficult and more useful than many people think. Lisa F. Young/Shutterstock.com

The father writes the mothers age on a slip of paper and turns the slip over so the boy cannot see the numeral. He then lays the slip, blank side up, on a tablet. Next to the slip he writes the symbols that will help solve the problem:

The son takes only a moment to guess that his mother is 32 years old. When the father turns the slip of paper over, they see this answer is correct:

This will have been the boys first lesson in algebra because he essentially solved the equation x + 6 = 38.

The father did not say anything about a mysterious letter x that can stand for any number. Nor did he tell the boy about any rule such as changing the sign of the six and writing it on the other side of the equation. Instead, the boys first lesson in algebra evolved in a natural way from a problem in arithmetic.

When you study algebra in school, you will learn more about the relationship between algebra and arithmetic. Some of the fundamental concepts of algebra that are taught in school are explained in the following chapters. You will learn why algebra was developed; basic principles of algebra, such as variables, generalizations, and patterns; and everything you need to know about real numbers. More important, you will learn how to apply algebras fundamental concepts. In no time at all, algebra will cease to be a mystery.

A lgebra has often been described as arithmetic with letters. Unlike arithmetic, which deals with specific numbers, algebra introduces variables that greatly extend the generality and scope of arithmetic. This book will focus on the algebra taught in middle schools and high schools, often referred to as elementary algebra, which deals with the general properties of numbers and the relations between them.

ALGEBRAIC QUANTITIES

The principal distinguishing characteristic of algebra is the use of letters to represent numerical quantities and simple symbols to represent mathematical operations. Following a system that originated with the 17th-century French thinker Ren Descartes, letters, especially x, y, and z, represent unknown quantities, or variables. The + and signs indicate addition and subtraction of these quantities, but multiplication is simply indicated by adjacent letters. Thus, ax represents the product of a by x. This simple expression can be interpreted, for example, as the interest earned in one year by a sum of a dollars invested at an annual rate of x. It can also be interpreted as the distance traveled in a hours by a car moving at x miles per hour. Such flexibility of representation is what gives algebra its great utility.

THE BEGINNINGS OF ALGEBRA

More than 3,500 years ago an Egyptian named Ahmes collected a set of mathematical problems and their solutions. About 2,500 years ago the Greek mathematician Pythagoras started a religious-mathematical brotherhood. Intensely interested in geometry, they classified numbers according to geometrical properties. The famous Greek geometer Euclid discovered important properties of numbers through a study of geometry.

Diophantus, another famous early Greek mathematician, has been called the father of algebra. He treated algebra from a purely numerical point of view. He made a special study of certain types of equations that are today called Diophantine equations.

Our modern word algebra comes from the Arabic al-jabr, which appeared in the title of an algebra text written in about 825 CE by the Arab astronomer and mathematician al-Khwarizmi. The word algorithm is derived from his name.