Christian Voigt - Complex Semisimple Quantum Groups and Representation Theory
Here you can read online Christian Voigt - Complex Semisimple Quantum Groups and Representation Theory full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2020, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Complex Semisimple Quantum Groups and Representation Theory
- Author:
- Publisher:Springer
- Genre:
- Year:2020
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Complex Semisimple Quantum Groups and Representation Theory: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Complex Semisimple Quantum Groups and Representation Theory" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This book provides a thorough introduction to the theory of complex semisimple quantum groups, that is, Drinfeld doubles of q-deformations of compact semisimple Lie groups. The presentation is comprehensive, beginning with background information on Hopf algebras, and ending with the classification of admissible representations of the q-deformation of a complex semisimple Lie group.
The main components are:
- a thorough introduction to quantized universal enveloping algebras over general base fields and generic deformation parameters, including finite dimensional representation theory, the Poincar-Birkhoff-Witt Theorem, the locally finite part, and the Harish-Chandra homomorphism,
- the analytic theory of quantized complex semisimple Lie groups in terms of quantized algebras of functions and their duals,
- algebraic representation theory in terms of category O, and
- analytic representation theory of quantized complex semisimple groups.
Given its scope, the book will be a valuable resource for both graduate students and researchers in the area of quantum groups.
Christian Voigt: author's other books
Who wrote Complex Semisimple Quantum Groups and Representation Theory? Find out the surname, the name of the author of the book and a list of all author's works by series.
Complex Semisimple Quantum Groups and Representation Theory — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Complex Semisimple Quantum Groups and Representation Theory" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
This series reports on new developments in all areas of mathematics and their applications - quickly, informally and at a high level. Mathematical texts analysing new developments in modelling and numerical simulation are welcome. The type of material considered for publication includes:
1. Research monographs 2. Lectures on a new field or presentations of a new angle in a classical field 3. Summer schools and intensive courses on topics of current research.
Texts which are out of print but still in demand may also be considered if they fall within these categories. The timeliness of a manuscript is sometimes more important than its form, which may be preliminary or tentative.
3. Summer schools and intensive courses on topics of current research.
Texts which are out of print but still in demand may also be considered if they fall within these categories. The timeliness of a manuscript is sometimes more important than its form, which may be preliminary or tentative.
More information about this series at http://www.springer.com/series/304
This Springer imprint is published by the registered company Springer Nature Switzerland AG.
The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland
The first author would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the programme Operator Algebras: Subfactors and Their Applications, where work on this paper was undertaken. This work was supported by EPSRC grant no. EP/K032208/1. The first author was supported by the Polish National Science Centre grant no. 2012/06/M/ST1/00169. This paper was partially supported by the grant H2020-MSCA-RISE-2015-691246-QUANTUM DYNAMICS. The second author was supported by the project SINGSTAR of the Agence Nationale de la Recherche, ANR-14-CE25-0012-01 and by the CNRS PICS project OpPsi. Both authors would also like to thank the Erwin Schrdinger Institute in Vienna, where some of the present research was undertaken.
The theory of quantum groups, originating from the study of integrable systems, has seen a rapid development from the mid 1980s with far-reaching connections to various branches of mathematics, including knot theory, representation theory and operator algebras, see [] is a powerful framework which allows one to extend Pontrjagin duality to a fully noncommutative setting.
In both the algebraic and the analytic theory of quantum groups, an important role is played by the Drinfeld double, also known as the quantum double, which is designed to produce solutions to the quantum Yang-Baxter equation. The algebraic version of this construction, due to Drinfeld, appears already in [].
If one applies the Drinfeld double construction to the Hopf algebra of functions on the q-deformation of a compact semisimple Lie group, then, in accordance with the quantum duality principle [] in the case of the quantum Lorentz group 
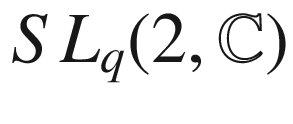, is key to understanding the structure of these Drinfeld doubles. More precisely, one can transport techniques from the representation theory of classical complex semisimple groups to the quantum situation, and it turns out that the main structural results carry over, albeit with sometimes quite different proofs.
These notes contain an introduction to the theory of complex semisimple quantum groups, that is, Drinfeld doubles of compact quantum groups arising from q-deformations. Our main aim is to present the classification of irreducible Harish-Chandra modules for these quantum groups, or equivalently the irreducible Yetter-Drinfeld modules of
Font size:
Interval:
Bookmark:
Similar books «Complex Semisimple Quantum Groups and Representation Theory»
Look at similar books to Complex Semisimple Quantum Groups and Representation Theory. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Discussion, reviews of the book Complex Semisimple Quantum Groups and Representation Theory and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.