LIE ALGEBRAS
by
NATHAN JACOBSON
Henry Ford II Professor of Mathematics
Yale University, New Haven, Connecticut
Dover Publications, Inc.
New York
Copyright 1962 by Nathan Jacobson.
All rights reserved.
Bibliographical Note
This Dover edition, first published in 1979, is an unabridged and corrected republication of the work originally published in 1962 by Interscience Publishers, a division of John Wiley & Sons, Inc.
International Standard Book Number
ISBN-13: 978-0-486-63832-4
ISBN-10: 0-486-63832-4
Manufactured in the United States by Courier Corporation
63832410
www.doverpublications.com
PREFACE
The present book is based on lectures which the author has given at Yale during the past ten years, especially those given during the academic year 19591960. It is primarily a textbook to be studied by students on their own or to be used for a course on Lie algebras. Besides the usual general knowledge of algebraic concepts, a good acquaintance with linear algebra (linear transformations, bilinear forms, tensor products) is presupposed. Moreover, this is about all the equipment needed for an understanding of the first nine chapters. For the tenth chapter, we require also a knowledge of the notions of Galois theory and some of the results of the Wedderburn structure theory of associative algebras.
The subject of Lie algebras has much to recommend it as a subject for study immediately following courses on general abstract algebra and linear algebra, both because of the beauty of its results and its structure, and because of its many contacts with other branches of mathematics (group theory, differential geometry, differential equations, topology). In this exposition we have tried to avoid making the treatment too abstract and have consistently followed the point of view of treating the theory as a branch of linear algebra. The general abstract notions occur in two groups: the first, adequate for the structure theory, in to the problem of sorting out the simple Lie algebras over an arbitrary field.
No attempt has been made to indicate the historical development of the subject or to give credit for individual contributions to it. In this respect we have confined ourselves to brief indications here and there of the names of those responsible for the main ideas. It is well to record here the authors own indebtedness to one of the great creators of the theory, Professor Hermann Weyl, whose lectures at the Institute for Advanced Study in 19331934 were truly inspiring and led to the authors research in this field. It should be noted also that in these lectures Professor Weyl, although primarily concerned with the Lie theory of continuous groups, set the subject of Lie algebras on its own independent course by introducing for the first time the term Lie algebra as a substitute for infinitesimal group, which had been used exclusively until then.
A fairly extensive bibliography is included; however, this is by no means complete. The primary aim in compiling the bibliography has been to indicate the avenues for further study of the topics of the book and those which are immediately related to it.
I am very much indebted to my colleague George Seligman for carefully reading the various versions of the manuscript and offering many suggestions for improving the exposition. Drs. Paul Cohn and Ancel Mewborn have also made valuable comments, and all three have assisted with the proofreading. I take this opportunity to offer all three my sincere thanks.
| May 28, 1961 | NATHAN JACOBSON |
| New Haven, Connecticut |
CONTENTS
LIE ALGEBRAS
CHAPTER I
Basic Concepts
The theory of Lie algebras is an outgrowth of the Lie theory of continuous groups. The main result of the latter is the reduction of local problems concerning Lie groups to corresponding problems on Lie algebras, thus to problems in linear algebra. One associates with every Lie group a Lie algebra over the reals or complexes and one establishes a correspondence between the analytic subgroups of the Lie group and the subalgebras of its Lie algebra, in which invariant subgroups correspond to ideals, abelian subgroups to abelian subalgebras, etc. Isomorphism of the Lie algebras is equivalent to local isomorphism of the corresponding Lie groups. We shall not discuss these matters in detail since excellent modern accounts of the Lie theory are available. The reader may consult one of the following books: Chevalleys Theory of Lie Groups, Cohns Lie Groups, Pontrjagins Topological Groups.
More recently, two other types of group theory have been aided by the introduction of appropriate Lie algebras in their study. The first of these is the theory of free groups which can be studied by means of free Lie algebras using a method which was originated by Magnus. Although the connection here is not so close as in the Lie theory, significant results on free groups and other types of discrete groups have been obtained using Lie algebras. Particularly noteworthy are the results on the so-called restricted Burnside problem: Is there a bound for the orders of the finite groups with a fixed number r of generators and satisfying the relation xm = 1, m a fixed positive integer? It is worth mentioning that Lie algebras of prime characteristic play an important role in these applications to discrete group theory. Again we shall not enter into the details but refer the interested reader to two articles which give a good account of this method in group theory. These are: Lazard [2] and Higman [1].
The type of correspondence between subgroups of a Lie group and subalgebras of its Lie algebra which obtains in the Lie theory has a counterpart in Chevalleys theory of linear algebraic groups. Roughly speaking, a linear algebraic group is a subgroup of the group of non-singular nn matrices which is specified by a set of polynomial equations in the entries of the matrices. An example is the orthogonal group which is defined by the set of equations 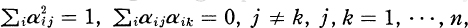 on the entries ij of the matrix (ij). With each linear algebraic group Chevalley has defined a corresponding Lie algebra (see Chevalley [2]) which gives useful information on the group and is decisive in the theory of linear algebraic groups of characteristic zero.
on the entries ij of the matrix (ij). With each linear algebraic group Chevalley has defined a corresponding Lie algebra (see Chevalley [2]) which gives useful information on the group and is decisive in the theory of linear algebraic groups of characteristic zero.
In view of all this group theoretic background it is not surprising that the basic concepts in the theory of Lie algebras have a group-theoretic flavor. This should be kept in mind throughout the study of Lie algebras and particularly in this chapter, which gives the foundations that are adequate for the main structure theory to be developed in .
1. Definition and construction of Lie and associative algebras
We recall the definition of a non-associative algebra (= not necessarily associative algebra)  over a field . This is just a vector space
over a field . This is just a vector space  over in which a bilinear composition is defined. Thus for every pair (x, y), x, y in
over in which a bilinear composition is defined. Thus for every pair (x, y), x, y in  , we can associate a product x y
, we can associate a product x y













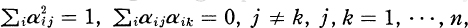 on the entries ij of the matrix (ij). With each linear algebraic group Chevalley has defined a corresponding Lie algebra (see Chevalley [2]) which gives useful information on the group and is decisive in the theory of linear algebraic groups of characteristic zero.
on the entries ij of the matrix (ij). With each linear algebraic group Chevalley has defined a corresponding Lie algebra (see Chevalley [2]) which gives useful information on the group and is decisive in the theory of linear algebraic groups of characteristic zero. over a field . This is just a vector space
over a field . This is just a vector space