Contents
Guide

Pietro Giuseppe Fr, Alexander Fedotov
Groups and Manifolds
Also of Interest

Multivariable Calculus and Differential Geometry
Gerard Walschap, 2015
ISBN 978-3-11-036949-6, e-ISBN 978-3-11-036954-0

Tensors and Riemannian Geometry
With Applications to Differential Equations
Nail H. Ibragimov, 2015
ISBN 978-3-11-037949-5, e-ISBN 978-3-11-037950-1

Symmetry
Through the Eyes of Old Masters
Emil Makovicky, 2016
ISBN 978-3-11-041705-0, e-ISBN: 978-3-11-041714-2

Series: De Gruyter Studies in Mathematical Physics
M. Efroimsky, L. Gamberg, D. Gitman, A. Lazarian, B. M. Smirnov
ISSN 2194-3532
Published titles in this series:
Vol. 42: Javier Roa: Regularization in Orbital Mechanics (2017)
Vol. 39: Vladimir K. Dobrev: Invariant Differential Operators 2 (2017)
Vol. 35: Vladimir K. Dobrev: Invariant Differential Operators 1 (2016)

Authors
Prof. Pietro Giuseppe Fr
Universit degli Studi di Torino
Via P. Giuria 1
10125 Torino
Italy
pietro.fre@esteri.it
Dr Alexander Fedotov
Department of Theoretical Physics
National Research Nuclear University MEPhI
Kashirskoe Shosse 31
Moscow 115409
Russia
AMFedotov@MEPhI.ru
ISBN 978-3-11-055119-8
e-ISBN (PDF) 978-3-11-055120-4
e-ISBN (EPUB) 978-3-11-055133-4
Library of Congress Cataloging-in-Publication Data
A CIP catalog record for this book has been applied for at the Library of Congress.
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.
2018 Walter de Gruyter GmbH, Berlin/Boston
www.degruyter.com

This book is dedicated from the part of Pietro Fr to his beloved daughter Laura, to his darling wife Olga and to his younger son Vladimir. On the part of Alexander Fedotov it is dedicated to his darling wife Evgenya and to his beloved daughters Ekaterina and Anna.
Preface
The present book has its initial basis in the course on Lie Algebras and Lie Groups that one of us (P.F.) used to give at SISSA when he was Professor of Theoretical Physics there in the years 19901996. The stimulus to revise and update those lecture notes to the point of writing a self-contained book on such topics came more recently when it was agreed that P.F., working several years in Moscow as scientific attach of the Italian Embassy, would give a course on Groups and Symmetries at the National Research Nuclear University MEPhI of Moscow. Further momentum the project gained from the association of the first with the second author (A.F.) who conducted weekly sessions of exercises and problems, attached to the Course.
A further motivation to write these introductory Lectures on Groups and Manifolds for Physicists came by the imminent publication of other two more advanced books written by the first author for Springer Verlag, namely:
- Advances in Lie Algebras and Geometry from Supergravity .
- A Conceptual History of Symmetry from Plato to Special Geometries .
Symmetry is the keyword underpinning our modern understanding of the Fundamental Laws of Nature and it is also the central focus of most mathematical disciplines, of which Geometry, in this respect, is at the top of the priority list.
By the wording The Mathematics of Symmetry , every contemporary Mathematician and Physicist understands Lie Algebras, Lie Groups, Coset Manifolds and also Discrete and Finite Groups . There is no doubt that such topics are classical and constitute the backbone in the education of students in theoretical physics so that many excellent textbooks exist on the market that have been written both by mathematicians and by physicists. Yet, notwithstanding their established classical status, research continues in these mathematical fields and many developments have taken place in the last twenty years, several of them stimulated and directed by developments in supersymmetric field theories, supergravity and superstrings. As the first author advocates in the above quoted two books, the mathematical needs of the super-world have promoted an extensive reframing and a deeper understanding of many chapters in the Mathematics of Symmetry , leading to new conceptions that usually are not reflected in the existing textbook literature. As their title suggest, the above quoted two books deal with the task of presenting in a modern unified way the Advances in Geometry and Lie Algebra Theory that are most relevant to contemporary field theories, the supersymmetric ones having top priority. Parallel aim in the writing was that of presenting the conceptual evolution of the episteme from ancient times to the contemporary vision. Indeed, trying to summarize the implications for the episteme of the last thirty-three years of experimental physics, the first author arrived at the following conclusion.
Leaving apart the issue of quantization , that we can generically identify with the functional path integral over classical configurations , we have, within our contemporary physical paradigm, a rather simple and universal scheme of interpretation of the Fundamental Interactions and of the Fundamental Constituents of Matter based on the following few principles:
A) The categorical reference frame is provided by Field Theory defined by some action A=ML(,) 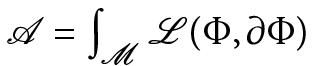 where L(,)
where L(,) 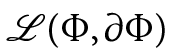 denotes some Lagrangian depending on a set of fields ( x ).
denotes some Lagrangian depending on a set of fields ( x ).
B) All fundamental interactions are described by connections A on principal fiber-bundles P (G, M ) where G is a Lie group and the base manifold M is some space-time in d = 4 or in higher dimensions .
C) All the fields describing fundamental constituents are sections of vector bundles B (G, V , M ) , associated with the principal one P (G, M ) and determined by the choice of suitable linear representations D (G) V V of the structural group G.
D) The spin zero particles, described by scalar fields I , have the additional feature of admitting non-linear interactions encoded in a scalar potential V () for whose choice general principles, supported by experimental confirmation, have not yet been determined .





















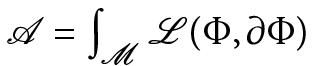 where L(,)
where L(,) 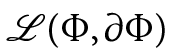 denotes some Lagrangian depending on a set of fields ( x ).
denotes some Lagrangian depending on a set of fields ( x ).