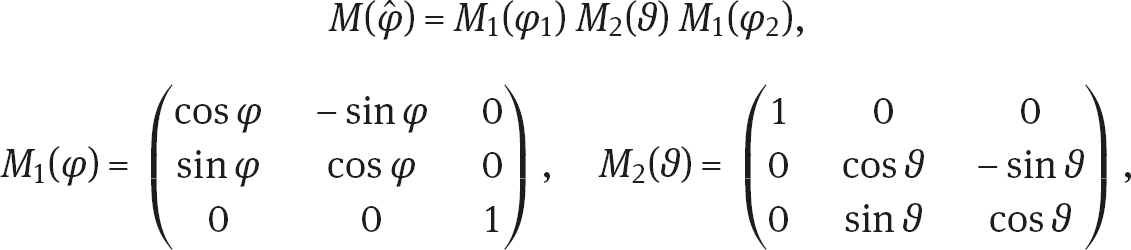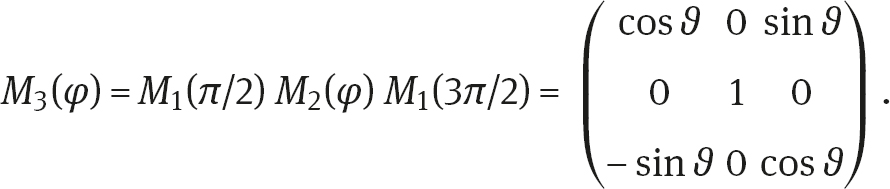Guide

Vladimir K. Dobrev
Invariant Differential Operators
De Gruyter Studies in Mathematical Physics
Edited by
Michael Efroimsky, Bethesda, Maryland, USA
Leonard Gamberg, Reading, Pennsylvania, USA
Dmitry Gitman, So Paulo, Brazil
Alexander Lazarian, Madison, Wisconsin, USA
Boris Smirnov, Moscow, Russia
Volume 35

Mathematics Subject Classification 2010
17BXX, 17B45, 17B35, 17B67, 17B81, 16S30, 22EXX, 22E47, 22E15, 22E60, 81R05, 81R10, 32M15, 47A15, 47A46, 53A55, 70H33
Author
Prof. Vladimir K. Dobrev
Bulgarian Academy of Sciences
Institute for Nuclear Research
and Nuclear Energy
Tsarigradsko Chaussee 72
1784 SOFIA
Bulgaria
http://theo.inrne.bas.bg/dobrev/
ISBN 978-3-11-043542-9
e-ISBN (PDF) 978-3-11-042764-6
e-ISBN (EPUB) 978-3-11-042780-6
Set-ISBN 978-3-11-042765-3
ISSN 2194-3532
Library of Congress Cataloging-in-Publication Data
A CIP catalog record for this book has been applied for at the Library of Congress.
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.
2016 Walter de Gruyter GmbH, Berlin/Boston
Typesetting: Integra Software Services Pvt. Ltd.
www.degruyter.com
Preface
Invariant differential operators play a very important role in the description of physical symmetries recall, e.g., the examples of Dirac, Maxwell, KleinGordon, dAlmbert, and Schrdinger equations. Invariant differential operators played and continue to play important role in applications to conformal field theory. Invariant superdifferential operators were crucial in the derivation of the classification of positive energy unitary irreducible representations of extended conformal supersymmetry first in four dimensions, then in various dimensions. Last, but not least, among our motivations are the mathematical developments in the last 50 years and counting.
Obviously, it is important for the applications in physics to study these operators systematically. A few years ago we have given a canonical procedure for the construction of invariant differential operators. Lately, we have given an explicit description of the building blocks, namely, the parabolic subgroups and subalgebras from which the necessary representations are induced.
Altogether, over the years we have amassed considerable material which was suitable to be exposed systematically in book form. To achieve portable formats, we decided to split the book in two volumes. In the present first volume, our aim is to introduce and explain our canonical procedure for the construction of invariant differential operators and to explain how they are used on many series of examples. Our objects are noncompact semisimple Lie algebras, and we study in detail a family of those that we call conformal Lie algebras since they have properties similar to the classical conformal algebras of Minkowski space-time. Furthermore, we extend our considerations to simple Lie algebras that are called parabolically related to the initial family.
The second volume will cover various generalizations of our objects, e.g., the AdS/CFT correspondence, quantum groups, superalgebras, infinite-dimensional (super-)algebras including (super-)Virasoro algebras, and (q-)Schrdinger algebras.
Contents
1Introduction
1.1Symmetries
The notion of symmetry is a very old one. This is not surprising since there are many natural objects and living beings
which possess symmetry. So since the beginning of civilization people were influenced by this, and by 1200 B.C. symmetry was used extensively in Greek art. These were usually geometric symmetries such as discrete translational symmetry (when some figures were repeated from left to right (or top to bottom)); reflection symmetry with respect to some axis
(combined with translational symmetry); and discrete rotational symmetry (when a figure is not changed upon rotation of a fixed angle).
From the arts the notion of symmetry passed to the sciences. For instance, some symmetrical geometrical figures such as the circle and sphere were considered perfect by the Pythagoreans.
Of course, it was clear that the real world is not exactly symmetric e.g., take the human body as a nonexact symmetry.
The first appearances of symmetry in physics were of geometric nature. It was natural to think that the fundamental constituents of nature should possess some of these symmetries. Indeed, this is the case for many crystals and molecules, which in many cases are symmetrically arranged with respect to reflections as well as discrete translations and rotations. To this day, the study of such discrete symmetries is an interesting field of science.
The use of symmetries in mathematics and physics was enhanced when it was fully realized that symmetries can be described mathematically by expressing a set of transformations that leave a particular structure unchanged. This was especially important for the use of continuous symmetries .
Thus the set of transformations which leaves the sphere unchanged is the set of rotations of arbitrary angle around the three axes in a three-dimensional Euclidean space.
Mathematically, this is expressed as follows. The sphere of radius r ( 0) with the center at the beginning of the coordinate system is described as the points with coordinates x , x , x so that
which can be written in matrix form as
and the fact that the rotations are preserving the sphere may be expressed as
where the 3 3 matrices 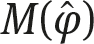 depend on the three angles of rotation in the three possible planes in three dimensions, which is symbolically denoted by
depend on the three angles of rotation in the three possible planes in three dimensions, which is symbolically denoted by 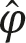 .
.
Using so-called Euler angles , , , the explicit dependence on the rotation angles is shown as follows:
where M and M are rotations in the planes ( x , x ) and ( x , x ), respectively, while the rotations in the plane ( x , x ) are given by

















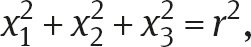
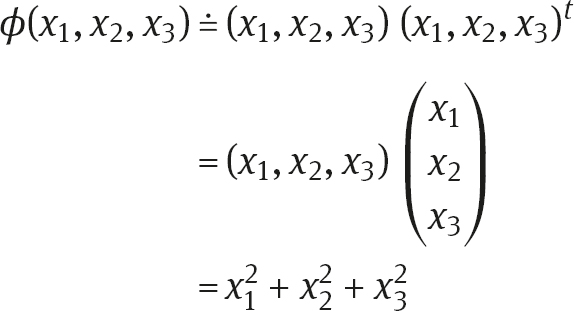
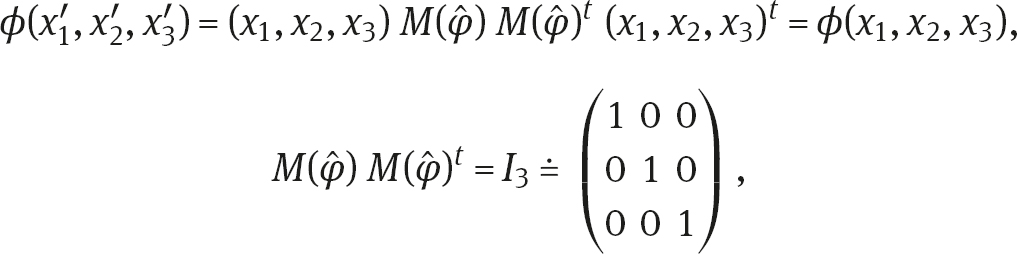
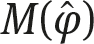 depend on the three angles of rotation in the three possible planes in three dimensions, which is symbolically denoted by
depend on the three angles of rotation in the three possible planes in three dimensions, which is symbolically denoted by 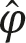 .
.