David J Winter - Abstract Lie Algebras
Here you can read online David J Winter - Abstract Lie Algebras full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 1972, publisher: INscribe Digital;Dover Publications, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Abstract Lie Algebras
- Author:
- Publisher:INscribe Digital;Dover Publications
- Genre:
- Year:1972
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Abstract Lie Algebras: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Abstract Lie Algebras" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Solid but concise, this account of Lie algebra emphasizes the theorys simplicity and offers new approaches to major theorems. Author David J. Winter, a Professor of Mathematics at the University of Michigan, also presents a general, extensive treatment of Cartan and related Lie subalgebras over arbitrary fields.
Preliminary material covers modules and nonassociate algebras, followed by a compact, self-contained development of the theory of Lie algebras of characteristic 0. Topics include solvable and nilpotent Lie algebras, Cartan subalgebras, and Levis radical splitting theorem and the complete reducibility of representations of semisimple Lie algebras. Additional subjects include the isomorphism theorem for semisimple Lie algebras and their irreducible modules, automorphism of Lie algebras, and the conjugacy of Cartan subalgebras and Borel subalgebras. An extensive theory of Cartan and related subalgebras of Lie algebras over arbitrary fields is developed in the final...
David J Winter: author's other books
Who wrote Abstract Lie Algebras? Find out the surname, the name of the author of the book and a list of all author's works by series.













 is a set and k a field.
is a set and k a field.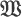 over k together with a mapping
over k together with a mapping  , denoted
, denoted 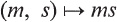 , such that (m + n)s = (ms) + (ns) for
, such that (m + n)s = (ms) + (ns) for 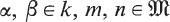 , and
, and  .
.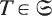 . Then TM is the linear transformation of
. Then TM is the linear transformation of  .
.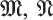 over k is the
over k is the  of the vector spaces
of the vector spaces  defined by
defined by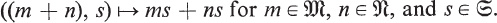
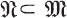 , we let
, we let  be the subspace of
be the subspace of 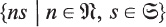 .
.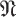 of
of  . Such an
. Such an 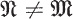 and
and 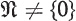
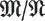 of
of