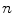Matej Bresar - Introduction to Noncommutative Algebra
Here you can read online Matej Bresar - Introduction to Noncommutative Algebra full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2014, publisher: Springer, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Introduction to Noncommutative Algebra
- Author:
- Publisher:Springer
- Genre:
- Year:2014
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Introduction to Noncommutative Algebra: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Introduction to Noncommutative Algebra" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Providing an elementary introduction to noncommutative rings and algebras, this textbook begins with the classical theory of finite dimensional algebras. Only after this, modules, vector spaces over division rings, and tensor products are introduced and studied. This is followed by Jacobsons structure theory of rings. The final chapters treat free algebras, polynomial identities, and rings of quotients.
Many of the results are not presented in their full generality. Rather, the emphasis is on clarity of exposition and simplicity of the proofs, with several being different from those in other texts on the subject. Prerequisites are kept to a minimum, and new concepts are introduced gradually and are carefully motivated. Introduction to Noncommutative Algebra is therefore accessible to a wide mathematical audience. It is, however, primarily intended for beginning graduate and advanced undergraduate students encountering noncommutative algebra for the first time.
Matej Bresar: author's other books
Who wrote Introduction to Noncommutative Algebra? Find out the surname, the name of the author of the book and a list of all author's works by series.













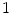 to indicate that it plays the role of a unity, requires that the square of the other one is
to indicate that it plays the role of a unity, requires that the square of the other one is 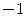 , and then extends this multiplication to the whole space by bilinearity. If one is interested in the geometric interpretation of this multiplication, then one will choose these two vectors more carefully. However, from the algebraic point of view it does not matter which two vectors we take, as long as they are linearly independent and therefore form a basis of our space. In any case we get a
, and then extends this multiplication to the whole space by bilinearity. If one is interested in the geometric interpretation of this multiplication, then one will choose these two vectors more carefully. However, from the algebraic point of view it does not matter which two vectors we take, as long as they are linearly independent and therefore form a basis of our space. In any case we get a 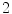 -dimensional
-dimensional 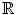 -algebra isomorphic to the complex number field
-algebra isomorphic to the complex number field 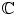 .
.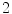 -dimensional spaces? Are there other ways to create some kind of numbers from finite dimensional real vector spaces? In any set of numbers one should be able to add, subtract, and multiply elements, and multiplication should be associative and bilinear. Thus, our space should in particular be an
-dimensional spaces? Are there other ways to create some kind of numbers from finite dimensional real vector spaces? In any set of numbers one should be able to add, subtract, and multiply elements, and multiplication should be associative and bilinear. Thus, our space should in particular be an 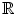 -algebra (in the early literature elements from algebras were actually called hypercomplex numbers ). In a decent set of numbers one should also be able to divide elements, with the obvious exclusion of dividing by
-algebra (in the early literature elements from algebras were actually called hypercomplex numbers ). In a decent set of numbers one should also be able to divide elements, with the obvious exclusion of dividing by 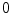 . We can now rephrase our question in a rigorous manner as follows: Is it possible to define multiplication on an
. We can now rephrase our question in a rigorous manner as follows: Is it possible to define multiplication on an 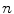 -dimensional real space so that it becomes a real division algebra?
-dimensional real space so that it becomes a real division algebra?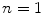 the question is trivial; every element is a scalar multiple of unity and therefore up to isomorphism
the question is trivial; every element is a scalar multiple of unity and therefore up to isomorphism 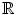 itself is the only such algebra. For
itself is the only such algebra. For 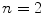 we know one example,
we know one example, 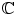 , but are there any other? This question is quite easy and the reader may try to solve it immediately. What about
, but are there any other? This question is quite easy and the reader may try to solve it immediately. What about 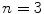 ? This is already a nontrivial question, but certainly a natural and challenging one. After finding a multiplication in 2-dimensional spaces of such enormous importance in mathematics, should not the next step be finding something similar in
? This is already a nontrivial question, but certainly a natural and challenging one. After finding a multiplication in 2-dimensional spaces of such enormous importance in mathematics, should not the next step be finding something similar in 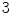 -dimensional spaces? Furthermore, what about
-dimensional spaces? Furthermore, what about 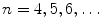 ?
?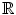 -algebra . We will find all possible
-algebra . We will find all possible 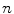 for which such an algebra exists, and moreover, all possible multiplications making a finite dimensional real space into a division algebra.
for which such an algebra exists, and moreover, all possible multiplications making a finite dimensional real space into a division algebra.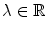 , we write
, we write 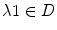 simply as
simply as 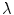 . In fact we identify
. In fact we identify 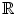 with
with 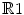 , and in this way consider
, and in this way consider 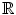 as a subalgebra of
as a subalgebra of 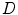 .
.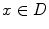 there exists
there exists 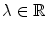 such that
such that 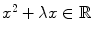 .
.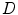 is
is 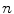 , the elements
, the elements 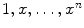 are linearly dependent. This means that there exists a nonzero polynomial
are linearly dependent. This means that there exists a nonzero polynomial 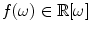 of degree at most
of degree at most