Fundamental Concepts
of Abstract Algebra
G ERTURDE E HRLICH
The University of Maryland
D OVER P UBLICATIONS , I NC .
Mineola, New York
Copyright
Copyright 1991 by Gertrude Ehrlich.
All rights reserved.
Bibliographical Note
This Dover edition, first published in 2011, is an unabridged republication of the work originally published in 1991 by PWS-Kent Publishing Company, Boston.
Library of Congress Cataloging-in-Publication Data
Ehrlich, Gertrude.
Fundamental concepts of abstract algebra / Gertrude Ehrlich. Dover ed.
p. cm.
Originally published: Boston : PWS-Kent Pub., 1991.
Includes bibliographical references and index.
ISBN-13: 978-0-486-48589-8 (pbk.)
ISBN-10: 0-486-48589-7 (pbk.)
1. Algebra, Abstract. I. Title.
QA162.E37 2011
512'.02dc23
2011019127
Manufactured in the United States by Courier Corporation
48589701
www.doverpublications.com
All right, said the Cat; and this time it vanished quite slowly, beginning with the end of the tail, and ending with the grin, which remained some time after the rest of it had gone.
Well! Ive often seen a cat without a grin, thought Alice, but a grin without a cat! Its the most curious thing I ever saw in all my life!
(Lewis Carroll, Alice in Wonderland )

Preface
 his book is intended as a text in abstract algebra for undergraduate mathematics majors. It contains ample material for a two-semester sequence, including a thorough treatment of field theory during the second semester. Some knowledge of the rudiments of linear algebra is assumed from the start, and a fair number of examples are drawn from this area. In Sections 1017 of , finite-dimensional vector spaces are treated in an abstract algebraic setting. These sections may be used for review, for reference, or to enhance the linear algebra background of the students. Some possible two-semester sequences are described below.
his book is intended as a text in abstract algebra for undergraduate mathematics majors. It contains ample material for a two-semester sequence, including a thorough treatment of field theory during the second semester. Some knowledge of the rudiments of linear algebra is assumed from the start, and a fair number of examples are drawn from this area. In Sections 1017 of , finite-dimensional vector spaces are treated in an abstract algebraic setting. These sections may be used for review, for reference, or to enhance the linear algebra background of the students. Some possible two-semester sequences are described below.
The exercise list in each section of each chapter starts with an exercise consisting of True-or-False statements, selected with the aim of inducing a thoughtful review of materials covered in the section, and dispelling misconceptions at an early stage.
Possible Two-Semester Sequences:
Model 1 (including a full treatment of Galois Theory)
First Semester:
(13)
(111; 12, 13 if time permits)
(19; 10 if time permits)
Second Semester:
(14, 15)
(117)
Model 2 (including some field theory , but not Galois theory , and an introduction to abstract linear algebra)
First Semester:
(13)
(111)
(18)
Second Semester:
(1215)
(917)
(15)

Acknowledgements
 am deeply indebted to my colleagues, Professors John Horvath, Adam Kleppner, and David Schneider, who taught from the manuscript and made many valuable comments; to numerous students, notably Greg Grant and Aaron Naiman (champion error finders); and to Kristi Aho Kraft and Virginia Sauber Vargas who typed a large portion of the manuscript, with much skill and forbearance.
am deeply indebted to my colleagues, Professors John Horvath, Adam Kleppner, and David Schneider, who taught from the manuscript and made many valuable comments; to numerous students, notably Greg Grant and Aaron Naiman (champion error finders); and to Kristi Aho Kraft and Virginia Sauber Vargas who typed a large portion of the manuscript, with much skill and forbearance.
I would also like to express my appreciation to the following reviewers: Daniel D. Anderson (University of Iowa), Ida Z. Arms (Indiana University of Pennsylvania), Robert Beezer (University of Puget Sound), Patrick J. Costello (Eastern Kentucky University), John C. Higgins (Brigham Young University), Frederick Hoffman (Florida Atlantic University), William J. Keane (Boston College), Daniel B. Shapiro (Ohio State University), Anita A. Solow (Grinnell College), John R. Stallings (University of California-Berkeley), Paul M. Weichsel (University of Illinois), and Anne Ludington Young (Loyola College).

Glossary of Symbols

| The set of all integers, rational numbers, real numbers, and complex numbers, respectively. |
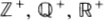
| The set of all positive integers, rational numbers, and real numbers, respectively. |
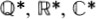
| The set of all non-zero rational numbers, real numbers, and complex numbers, respectively. |
Mn ( A ) | The set of all n n matrices with entries in A . |
GLn(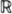 ) ) | The set of all non-singular n n matrices with real entries. |
SLn(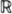 ) ) | The set of all n n matrices with real entries and with determinant equal to 1. |

| Is a subset of. |

| Contains as a subset. |
Is an element of. |
f : A B | f is a function from A to B . |

Contents

 he following historical remarks are intended to be read at the outset of your study, and then reread from time to time as your knowledge of the subject increases.
he following historical remarks are intended to be read at the outset of your study, and then reread from time to time as your knowledge of the subject increases.

Abstraction Is Power
Much of the power of mathematics stems from its abstractness, which is the source of its universality. Mathematics was abstract from its very beginnings in prehistoric times. Primitive humans, confronted (through millions of years) with examples of sets such as these,
Figure 1
gradually learned to abstract from the differences of such sets, and to recognize a common property: threeness. In this way, through many acts of abstraction, they created the natural numbers. The abstract concepts 1, 2, 3, 4, 5, 6,...enabled them to deal more efficiently with concrete problems such as: if to  , I add
, I add  , how many cows will I have? If to
, how many cows will I have? If to 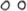
Next page














 his book is intended as a text in abstract algebra for undergraduate mathematics majors. It contains ample material for a two-semester sequence, including a thorough treatment of field theory during the second semester. Some knowledge of the rudiments of linear algebra is assumed from the start, and a fair number of examples are drawn from this area. In Sections 1017 of , finite-dimensional vector spaces are treated in an abstract algebraic setting. These sections may be used for review, for reference, or to enhance the linear algebra background of the students. Some possible two-semester sequences are described below.
his book is intended as a text in abstract algebra for undergraduate mathematics majors. It contains ample material for a two-semester sequence, including a thorough treatment of field theory during the second semester. Some knowledge of the rudiments of linear algebra is assumed from the start, and a fair number of examples are drawn from this area. In Sections 1017 of , finite-dimensional vector spaces are treated in an abstract algebraic setting. These sections may be used for review, for reference, or to enhance the linear algebra background of the students. Some possible two-semester sequences are described below. am deeply indebted to my colleagues, Professors John Horvath, Adam Kleppner, and David Schneider, who taught from the manuscript and made many valuable comments; to numerous students, notably Greg Grant and Aaron Naiman (champion error finders); and to Kristi Aho Kraft and Virginia Sauber Vargas who typed a large portion of the manuscript, with much skill and forbearance.
am deeply indebted to my colleagues, Professors John Horvath, Adam Kleppner, and David Schneider, who taught from the manuscript and made many valuable comments; to numerous students, notably Greg Grant and Aaron Naiman (champion error finders); and to Kristi Aho Kraft and Virginia Sauber Vargas who typed a large portion of the manuscript, with much skill and forbearance.
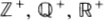
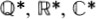
 )
)




 , I add
, I add  , how many cows will I have? If to
, how many cows will I have? If to