Christopher Norman - Finitely Generated Abelian Groups and Similarity of Matrices over a Field
Here you can read online Christopher Norman - Finitely Generated Abelian Groups and Similarity of Matrices over a Field full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: Springer, genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Finitely Generated Abelian Groups and Similarity of Matrices over a Field
- Author:
- Publisher:Springer
- Genre:
- Year:2012
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Finitely Generated Abelian Groups and Similarity of Matrices over a Field: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Finitely Generated Abelian Groups and Similarity of Matrices over a Field" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
At first sight, finitely generated abelian groups and canonical forms of matrices appear to have little in common. However, reduction to Smith normal form, named after its originator H.J.S.Smith in 1861, is a matrix version of the Euclidean algorithm and is exactly what the theory requires in both cases. Starting with matrices over the integers, Part 1 of this book provides a measured introduction to such groups: two finitely generated abelian groups are isomorphic if and only if their invariant factor sequences are identical. The analogous theory of matrix similarity over a field is then developed in Part 2 starting with matrices having polynomial entries: two matrices over a field are similar if and only if their rational canonical forms are equal. Under certain conditions each matrix is similar to a diagonal or nearly diagonal matrix, namely its Jordan form.
The reader is assumed to be familiar with the elementary properties of rings and fields. Also a knowledge of abstract linear algebra including vector spaces, linear mappings, matrices, bases and dimension is essential, although much of the theory is covered in the text but from a more general standpoint: the role of vector spaces is widened to modules over commutative rings.
Based on a lecture course taught by the author for nearly thirty years, the book emphasises algorithmic techniques and features numerous worked examples and exercises with solutions. The early chapters form an ideal second course in algebra for second and third year undergraduates. The later chapters, which cover closely related topics, e.g. field extensions, endomorphism rings, automorphism groups, and variants of the canonical forms, will appeal to more advanced students. The book is a bridge between linear and abstract algebra.
Christopher Norman: author's other books
Who wrote Finitely Generated Abelian Groups and Similarity of Matrices over a Field? Find out the surname, the name of the author of the book and a list of all author's works by series.













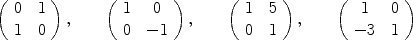
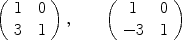
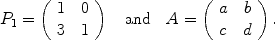
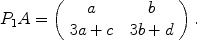
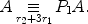
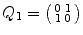 . Then
. Then 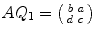 .
.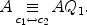

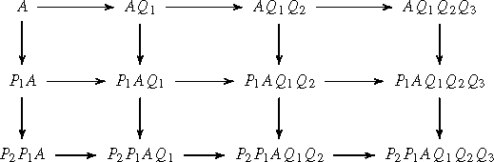
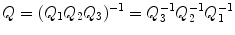 expresses Q as a product of elementary matrices. So P and Q are invertible over and satisfy
expresses Q as a product of elementary matrices. So P and Q are invertible over and satisfy