MATRIX THEORY
Joel N. Franklin
Professor of Applied Mathematics
California Institute of Technology DOVER PUBLICATIONS, INC. Mineola, New York
Copyright Copyright 1968, 1993 by Joel N. Franklin
All rights reserved.
Bibliographical Note This Dover edition of
Matrix Theory, first published in 2000, is a slightly corrected, unabridged republication of the book originally published under the same title in 1968 by Prentice-Hall, Inc., Englewood Cliffs, New Jersey.
Library of Congress Cataloging-in-Publication Data Franklin, Joel N.
Matrix theory / Joel N. Franklin. p. cm. Originally published: Englewood Cliffs, N.J. : Prentice-Hall, 1968, in series: Prentice-Hall series in applied mathematics.
Includes index. ISBN-13: 978-0-486-41179-8 ISBN-10: 0-486-41179-6 1. Matrices. I. Title. QA188.F66 2000
512.9434dc21 99-058316 Manufactured in the United States by Courier Corporation
41179603
www.doverpublications.com
PREFACE
The widespread applicability of high-speed digital computers has made it necessary for every modern engineer, mathematician, or scientist to have a knowledge of matrix theory.
The connection between digital computation and matrices is almost obvious. Matrices represent linear transformations from a finite set of numbers to another finite set of numbers. Since many important problems are linear, and since digital computers with a finite memory manipulate only finite sets of numbers, the solution of linear problems by digital computation usually involves matrices. This book developed from a course on matrix theory which I have given at Caltech since 1957. The course has been attended by graduate students, seniors, and juniors majoring in mathematics, economics, science, or engineering. The course was originally designed to be a preparation for courses in numerical analysis; but as the attendance increased through the years, I modified the syllabus to make it as useful as possible for the many different purposes of the students.
In many fieldsmathematical economics, quantum physics, geophysics, electrical network synthesis, crystallography, and structural engineering, to name a fewit has become increasingly popular to formulate and to solve problems in terms of matrices. Ten years ago there were few texts on matrices; now there are many texts, with different points of view. This text is meant to meet many different needs. Because the book is mathematically rigorous, it can be used by students of pure and applied mathematics. Because it is oriented towards applications, it can be used by students of engineering, science, and the social sciences. Because it contains the basic preparation in matrix theory required for numerical analysis, it can be used by students whose main interest is their future use of computers.
The book begins with a concise presentation of the theory of determinants. There follows a presentation of classical linear algebra, and then there is an optional chapter on the use of matrices to solve systems of linear differential equations. Next is a presentation of the most commonly used diagonalizations or triangularizations of Hermitian and non-Hermitian matrices. The following chapter presents a proof of the difficult and important matrix theorem of Jordan. Then there is a chapter on the variational principles and perturbation theory of matrices, which are used in applications and in numerical analysis. The book ends with a long chapter on matrix numerical analysis.
This last chapter is an introduction to the subject of linear computations, which is discussed in depth in the advanced treatises of Householder, Varga, Wilkinson, and others. The book presents certain topics which are relatively new in basic texts on matrix theory. There are sections on vector and matrix norms, on the condition-number of a matrix, on positive and irreducible matrices, on the numerical identification of stable matrices, and on the QR method for computing eigenvalues. A course on matrix theory lasting between one and two academic quarters could be based on selections from the first six chapters. A full-year course could cover the entire book. The book assumes very little mathematical preparation.
Except for the single section on the continuous dependence of eigenvalues on matrices, the book assumes only a knowledge of elementary algebra and calculus. The book begins with the most elementary results about determinants, and it proceeds gradually to cover the basic preparation in matrix theory which is necessary for every modern mathematician, engineer, or scientist. I wish to thank Dr. George Forsythe and Dr. Richard Dean for reading parts of the manuscript and for suggesting the inclusion of certain special topics. JOEL N.
FRANKLIN Pasadena, California
NOTATION USED IN THIS BOOK
Some authors denote vectors by boldface (
x,
y,
z), but we shall simply denote them by using lower-case English letters (
x,
y,
z). If we wish to designate the components of a vector,
x, we shall use subscripts; thus,
x1,... ,
xn designates the components of
x. Superscripts will be used to designate different vectors; thus,
x1,
x2,
x3 designates three vectors, and if there appears to be any chance of confusion with the powers of a scalar, we shall enclose the superscripts in parenthesese.g.,
x(1),
x(2),
x(3). Thus,
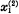
,... ,
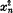
designates the squares of the
n components of a vector
x. ,
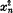
designates the squares of the
n components of a vector
x.
Matrices will be denoted by capital letters (A,B, C). Subscripts may be used to designate different matricese.g., A1, A2, A3,... but A, A2, A3 will designate different powers of the same square matrix, A. Thus, 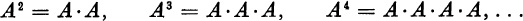 A lower case Greek lettere.g., , , will always designate an ordinary real or complex number. A Greek letter will never be used to designate a vector or a matrix. , cnto designate real or complex numbers. , cnto designate real or complex numbers.
A lower case Greek lettere.g., , , will always designate an ordinary real or complex number. A Greek letter will never be used to designate a vector or a matrix. , cnto designate real or complex numbers. , cnto designate real or complex numbers.
Subscripted English letters will never be used to designate vectors; thus, z3 cannot designate a vector, although it may be used to designate the third component of a vector z. For the columns of a matrix A we will often use the notation a(1),... , a(n) or simply a1,... , an. For the components of a matrix A we will write aij. Sometimes we shall write 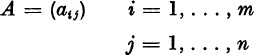 to indicate that A is the matrix
to indicate that A is the matrix 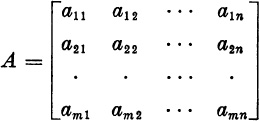 If A has the same number, n, of rows and columns, we may write
If A has the same number, n, of rows and columns, we may write 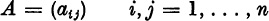 The rows of a matrix are horizontal; the columns are vertical. Thus,
The rows of a matrix are horizontal; the columns are vertical. Thus, 













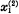 ,... ,
,... , 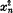 designates the squares of the n components of a vector x. ,
designates the squares of the n components of a vector x. , 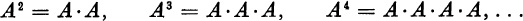 A lower case Greek lettere.g., , , will always designate an ordinary real or complex number. A Greek letter will never be used to designate a vector or a matrix. , cnto designate real or complex numbers. , cnto designate real or complex numbers.
A lower case Greek lettere.g., , , will always designate an ordinary real or complex number. A Greek letter will never be used to designate a vector or a matrix. , cnto designate real or complex numbers. , cnto designate real or complex numbers.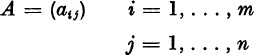 to indicate that A is the matrix
to indicate that A is the matrix 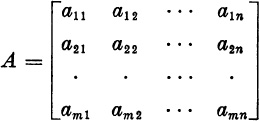 If A has the same number, n, of rows and columns, we may write
If A has the same number, n, of rows and columns, we may write 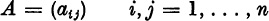 The rows of a matrix are horizontal; the columns are vertical. Thus,
The rows of a matrix are horizontal; the columns are vertical. Thus, 