Richard J. Lipton and Kenneth W. Regan
All rights reserved. No part of this book may be reproduced in any form or by any electronic or mechanical means (including photocopying, recording, or information storage and retrieval) without permission in writing from the publisher.
The MIT Press would like to thank the anonymous peer reviewers who provided comments on drafts of this book. The generous work of academic experts is essential for establishing the authority and quality of our publications. We acknowledge with gratitude the contributions of these otherwise uncredited readers.
Names: Lipton, Richard J., author. | Regan, Kenneth W., author.
Title: Introduction to quantum algorithms via linear algebra / Richard J. Lipton, Kenneth W. Regan.
Description: Second edition. | Cambridge, Massachusetts: The MIT Press, [2021]po | Includes bibliographical references and index.
Subjects: LCSH: Quantum computers. | Computer algorithms. | Algebras, Linear.
We dedicate this book to all those who helped create and nourish the beautiful area of quantum algorithms, and to our families, who helped create and nourish us.
Contents
List of Figures
Four-cycle graph G = C4, stochastic adjacency matrix G, and unitary matrix G.
Three-regular prism graph G and stochastic adjacency matrix .
Monotone circuit computing MAJ(x1,x2,x3,x4,x5).
Geometry of the circuit output.
Maze for Hadamard on qubit 1 followed by CNOT on 1 and 2.
Maze for two consecutive Hadamard gates.
Maze for Deutschs algorithm.
Maze stages for possible queried functions.
Maze for superdense coding.
Maze stages for Pauli operators on qubit 1.
Maze for quantum teleportation.
Three-polarizer paradox, illustrating the Born rule.
Cascaded Stern-Gerlach devices.
Born rule for polarized light.
The three-polarizer paradox. Shading indicates portions absorbed or passed through.
The Bloch sphere with axes and corresponding operators.
Basis-choice strategy for Alice and Bob in CHSH game.
Expanded graph G of quantum walk on path graph G.
Circuit for the HHL algorithm with n = 3 and L = 4. The t parts are many gates wide.
Approximation of 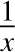 by a degree-13 polynomial. The vertical lines are at 0.22 and + 0.22.
by a degree-13 polynomial. The vertical lines are at 0.22 and + 0.22.
Preface to the First Edition
This book is an introduction to quantum algorithms unlike any other. It is short, yet it is comprehensive and covers the most important and famous quantum algorithms; it assumes minimal background, yet it is mathematically rigorous; it explains quantum algorithms, yet it steers clear of the notorious philosophical problems and issues of quantum mechanics.
We assume no background in quantum theory, quantum mechanics, or quantum anythingnone. Quantum computation can be described in terms of elementary linear algebra, so one needs familiarity with vectors, matrices, and their basic properties. However, we review all that we need from linear algebra, which is surprisingly little. If you need a refresher, then our material should be enough; if you are new to linear algebra, then we suggest some places where you can find the required material. It is really not much, so do not worry.
We do assume that you are comfortable with mathematical proofs; that is, we assume mathematical maturity in a way that is hard to define. Our proofs are short and straightforward, except for advanced topics in chapters 15 and 1719. [Chapter numbers are updated to the second edition.] This may be another surprise: for all the excitement about quantum algorithms, it is interesting that the mathematical tools and methods used are elementary. The proofs are neat, clever, and interesting, but you should have little trouble following the arguments. If you do, it is our faultwe hope that our explanations are always clear. Our idea of a standard course is part I, possibly adding chapter 16.
We strive for mathematical precision. There is always a fine line between being complete and clear and being pedanticwe hope we have stayed on the right side of this. We started with the principle of supplying all the detailsall of themon all we present. We have compromised in three places, all having to do with approximations. The first is our using the quantum Fourier transform as is rather than approximating it, and the others are in chapters 17 and 19.
For better focus on the algorithms, we chose to de-emphasize quantum circuits. We originally aimed to avoid quantum circuits and particularities of quantum gates altogether. However, they are excellent to illuminate linear algebra, so we have provided a rich set of exercises in chapters 37, plus two popular applications in section 8.3. These can in fact be used to support coverage of quantum circuits in a wider-scale course. The same goes for complexity classes. We prefer to speak operationally in terms of feasible computation, and we try to avoid being wedded to the asymptotically polynomially bounded definition of it. We avoid naming any complexity class until chapter 19. Nevertheless, that chapter has ample complexity content anchored in computational problems rather than machine models and can support a course that covers complexity theory. In addition, it gives algebraic tools for analyzing quantum circuits. We featured tricks we regard as algorithmic in the main text and delegated some tricks of implementation to exercises.
What makes an algorithm a quantum algorithm? The answer should have nothing to do with how the algorithm is implemented in a physical quantum system. We regard this as really a question about how programming notationmathematical notationrepresents the feasibility of calculations in nature. Quantum algorithms use algebraic units called qubits that are richer than bits: they are allowed to count as feasible some operations that, when written out in simple linear algebra, use exponentially long notation. The rules for these allowed operations are specified in standard models of quantum computation, which are all equivalent to the one presented in this book. It might seem ludicrous to believe that nature in any sense uses exponentially long notation, but some facet of this appears at hand because quantum algorithms can quickly solve problems that many researchers believe require exponential work by any classical algorithm. In this book, classical means an algorithm written in the notation for feasible operations used by every computer today.
This leads to a word about our presentation. Almost all summaries, notes, and books on quantum algorithms use a special notation for vectors and matrices. This is the famous Dirac notation that was invented by Paul Dirac (who else?). It has many advantages and is the de facto standard in the study of quantum algorithms. It is a great notation for experts and instrumental to becoming an expert, but we suspect it is a barrier for those starting out who are not experts. Thus, we avoid using it, except for a few places toward the end to give a second view of some complicated states. Our thesis is that we can explain quantum algorithms without a single use of this notation. Essentially, this book is a testament to that belief: if you find this book more accessible than others, then we believe it owes to this decision. Our notation follows certain ISO (International Organization for Standardization) recommendations, including boldface italics for vectors and heavy slant for matrices and operators.









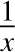 by a degree-13 polynomial. The vertical lines are at 0.22 and + 0.22.
by a degree-13 polynomial. The vertical lines are at 0.22 and + 0.22.