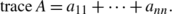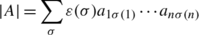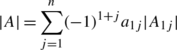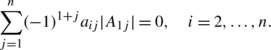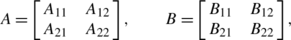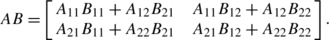• Complain
LitArk » Books » Science

Ravindra B. Bapat - Linear Algebra and Linear Models

Here you can read online Ravindra B. Bapat - Linear Algebra and Linear Models full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2012, publisher: Springer, genre: Science. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

Ravindra B. Bapat Linear Algebra and Linear Models
  • Book:
    Linear Algebra and Linear Models
  • Author:
  • Publisher:
    Springer
  • Genre:
  • Year:
    2012
  • Rating:
    4 / 5
  • Favourites:
    Add to favourites
  • Your mark:
    • 80
    • 1
    • 2
    • 3
    • 4
    • 5

Linear Algebra and Linear Models: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "Linear Algebra and Linear Models" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

Linear Algebra and Linear Models comprises a concise and rigorous introduction to linear algebra required for statistics followed by the basic aspects of the theory of linear estimation and hypothesis testing. The emphasis is on the approach using generalized inverses. Topics such as the multivariate normal distribution and distribution of quadratic forms are included.

For this third edition, the material has been reorganised to develop the linear algebra in the first six chapters, to serve as a first course on linear algebra that is especially suitable for students of statistics or for those looking for a matrix theoretic approach to the subject. Other key features include:

coverage of topics such as rank additivity, inequalities for eigenvalues and singular values;

a new chapter on linear mixed models;

over seventy additional problems on rank: the matrix rank is an important and rich topic with connections to many aspects of linear algebra such as generalized inverses, idempotent matrices and partitioned matrices.

This text is aimed primarily at advanced undergraduate and first-year graduate students taking courses in linear algebra, linear models, multivariate analysis and design of experiments. A wealth of exercises, complete with hints and solutions, help to consolidate understanding. Researchers in mathematics and statistics will also find the book a useful source of results and problems.

Ravindra B. Bapat: author's other books


Who wrote Linear Algebra and Linear Models? Find out the surname, the name of the author of the book and a list of all author's works by series.


Ravindra B. Bapat - Linear Algebra and Linear Models
Linear Algebra and Linear Models
Ravindra B. Bapat
Linear Algebra and Linear Models

Linear Algebra and Linear Models — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Linear Algebra and Linear Models" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make
1234567...62
R.B. Bapat Universitext Linear Algebra and Linear Models 3rd ed. 2012 10.1007/978-1-4471-2739-0_1 Springer-Verlag London Limited 2012
1. Vector Spaces and Subspaces
R. B. Bapat 1
(1)
Indian Statistical Institute, New Delhi, India
Abstract
Preliminaries concerning matrices and matrix operations are reviewed. Properties of determinant are recalled without proof. Vector spaces, linear independence, basis and dimension are introduced. It is shown that any two bases of a vector space have the same cardinality and that two vector spaces are isomorphic if and only if they have the same dimension. Extension of a linearly independent set to a basis is considered.
1.1 Preliminaries
In this chapter we first review certain basic concepts. We consider only real matrices. Although our treatment is self-contained, the reader is assumed to be familiar with the basic operations on matrices. We also assume knowledge of elementary properties of the determinant.
An m n matrix consists of mn real numbers arranged in m rows and n columns. The entry in row i and column j of the matrix A is denoted by a ij . An m 1 matrix is called a column vector of order m ; similarly, a 1 n matrix is a row vector of order n . An m n matrix is called a square matrix if m = n .
If A and B are m n matrices, then A + B is defined as the m n matrix with ( i , j )-entry a ij + b ij . If A is a matrix and c is a real number then cA is obtained by multiplying each element of A by c .
If A is m p and B is p n , then their product C = AB is an m n matrix with ( i , j )-entry given by
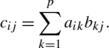
Linear Algebra and Linear Models - image 1
The following properties hold:
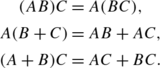
The transpose of the m n matrix A denoted by A is the n m matrix whose i - photo 2
The transpose of the m n matrix A , denoted by A , is the n m matrix whose ( i , j )-entry is a ji . It can be verified that ( A )= A , ( A + B )= A + B and ( AB )= B A .
A good understanding of the definition of matrix multiplication is quite useful. We note some simple facts which are often required. We assume that all products occurring here are defined in the sense that the orders of the matrices make them compatible for multiplication.
(i)
The j -th column of AB is the same as A multiplied by the j -th column of B .
(ii)
The i -th row of AB is the same as the i -th row of A multiplied by B .
(iii)
The ( i , j )-entry of ABC is obtained as
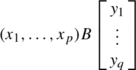
Linear Algebra and Linear Models - image 3
where ( x 1,, x p ) is the i -th row of A and ( y 1,, y q ) is the j -th column of C .
(iv)
If A =[ a 1,, a n ] and
Linear Algebra and Linear Models - image 4
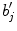where a i denote columns of A and Linear Algebra and Linear Models - image 5 denote rows of B , then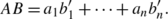
Linear Algebra and Linear Models - image 6
A diagonal matrix is a square matrix A such that a ij =0, i j . We denote the diagonal matrix
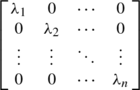
Linear Algebra and Linear Models - image 7
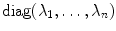by Linear Algebra and Linear Models - image 8 . When i =1 for all i , this matrix reduces to the identity matrix of order n , which we denote by I n or often simply by I , if the order is clear from the context. Observe that for any square matrix A , we have AI = IA = A .
The entries a 11,, a nn are said to constitute the (main) diagonal entries of A . The trace of A is defined as
Linear Algebra and Linear Models - image 9
It follows from this definition that if A , B are matrices such that both AB and BA are defined, then
Linear Algebra and Linear Models - image 10
The determinant of an n n matrix A , denoted by | A |, is defined as
where the summation is over all permutations 1 n of 1 n and is - photo 11
where the summation is over all permutations {(1),,( n )} of {1,, n } and () is 1 or 1 according as is even or odd.
We state some basic properties of determinant without proof:
(i)
The determinant can be evaluated by expansion along a row or a column. Thus, expanding along the first row,
where A 1 j is the submatrix obtained by deleting the first row and the j -th - photo 12
where A 1 j is the submatrix obtained by deleting the first row and the j -th column of A . We also note that
ii The determinant changes sign if two rows or columns are interchanged - photo 13
(ii)
The determinant changes sign if two rows (or columns) are interchanged.
(iii)
The determinant is unchanged if a constant multiple of one row is added to another row. A similar property is true for columns.
(iv)
The determinant is a linear function of any column (row) when all the other columns (rows) are held fixed.
(v)
| AB |=| A || B |.
The matrix A is upper triangular if a ij =0, i > j . The transpose of an upper triangular matrix is lower triangular .
It will often be necessary to work with matrices in partitioned form. For example, let
be two matrices where each A ij B ij is itself a matrix If compatibility for - photo 14
be two matrices where each A ij , B ij is itself a matrix. If compatibility for matrix multiplication is assumed throughout then we can write
12 Vector Spaces A nonempty set S is called a vector space if it satisfies the - photo 15
1.2 Vector Spaces
A nonempty set S is called a vector space if it satisfies the following conditions:
(i)
For any x , y in S , x + y is defined and is in S . Further,
ii There exists an element in S denoted by 0 such that x 0 x for all x - photo 16
(ii)
There exists an element in S , denoted by 0, such that x +0= x for all x .
(iii)
For any x in S there exists an element y in S such that x + y =0.
(iv)
For any x in S and any real number c , cx is defined and is in S ; moreover, 1 x = x for any x .
(v)
For any x 1, x 2 in S and reals c 1, c 2, c 1( x 1+ x 2)= c 1 x 1+ c 1 x 2, ( c 1+ c 2) x 1= c 1 x 1+ c 2 x 1 and c 1( c 2 x 1)=( c 1 c 2) x 1.
Elements in S are called vectors . If x , y are vectors then the operation of taking their sum x + y is referred to as vector addition. The vector in (ii) is called the zero vector. The operation in (iv) is called scalar multiplication . A vector space may be defined with reference to any field. We have taken the field to be the field of real numbers as this will be sufficient for our purpose.
Next page
1234567...62
Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make

Similar books «Linear Algebra and Linear Models»

Look at similar books to Linear Algebra and Linear Models. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.


No cover
No cover
Michael L. OLeary
Linear Algebra
No cover
No cover
Son
Linear Algebra Coding with Python: Pythons application for linear algebra
L. Shen - Linear Algebra
Linear Algebra
L. Shen
Linear Algebra
Jörg Liesen - Linear Algebra
Linear Algebra
Jörg Liesen
Linear Algebra
Ph.D. Shen - Linear Algebra
Linear Algebra
Ph.D. Shen
Linear Algebra
David J. Olive - Linear Regression
Linear Regression
David J. Olive
Linear Regression
N. H. Bingham - Regression: Linear Models in Statistics
Regression: Linear Models in Statistics
N. H. Bingham
Regression: Linear Models in Statistics
Paul A. Fuhrmann - A Polynomial Approach to Linear Algebra
A Polynomial Approach to Linear Algebra
Paul A. Fuhrmann
A Polynomial Approach to Linear Algebra
Georgi E. Shilov - Linear Algebra
Linear Algebra
Georgi E. Shilov
Linear Algebra
Kenneth M. Shiskowski - Principles of Linear Algebra with Mathematica
Principles of Linear Algebra with Mathematica
Kenneth M. Shiskowski
Principles of Linear Algebra with Mathematica
Franz E. Hohn - Elementary Matrix Algebra
Elementary Matrix Algebra
Franz E. Hohn
Elementary Matrix Algebra
Charles G. Cullen - Matrices and Linear Transformations: Second Edition
Matrices and Linear Transformations: Second Edition
Charles G. Cullen
Matrices and Linear Transformations: Second Edition
Reviews about «Linear Algebra and Linear Models»

Discussion, reviews of the book Linear Algebra and Linear Models and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.