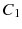One has to familiarize the student with actual questions from applications, so that he learns to deal with real world problems.
1.1 The PageRank Algorithm
The PageRank algorithm is a method to assess the importance of documents with mutual links , such as web pages, on the basis of the link structure. It was developed by Sergei Brin and Larry Page, the founders of Google Inc., at Stanford University in the late 1990s. The basic idea of the algorithm is the following:
Instead of counting links, PageRank essentially interprets a link of page A to page B as a vote of page A for page B. PageRank then assesses the importance of a page by the number of received votes. PageRank also considers the importance of the page that casts the vote, since votes of some pages have a higher value, and thus also assign a higher value to the page they point to. Important pages will be rated higher and thus lead to a higher position in the search results.
Let us describe (model) this idea mathematically. Our presentation uses ideas from the article [BryL06]. For a given set of web pages, every page k will be assigned an importance value
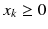
. A page k is more important than a page j if
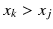
. If a page k has a link to a page j , we say that page j has a backlink from page k . In the above description these backlinks are the votes. As an example, consider the following link structure:
Here the page 1 has links to the pages 2, 3 and 4, and a backlink from page 3.
The easiest approach to define importance of web pages is to count its backlinks; the more votes are cast for a page, the more important the page is. In our example this gives the importance values
The pages 2 and 4 are thus the most important pages, and they are equally important.
However, the intuition and also the above description from Google suggests that backlinks from important pages are more important for the value of a page than those from less important pages. This idea can be modeled by defining
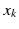
as the sum of all importance values of the backlinks of the page k . In our example this results in four equations that have to be satisfied simultaneously,
A disadvantage of this approach is that it does not consider the number of links of the pages. Thus, it would be possible to (significantly) increase the importance of a page just by adding links to that page. In order to avoid this, the importance values of the backlinks in the PageRank algorithm are divided by the number of links of the corresponding page. This creates a kind of internet democracy: Every page can vote for other pages, where in total it can cast one vote. In our example this gives the equations
These are four equations for the four unknowns, and all equations are linear ,.
For completeness, we mention that a solution for the four unknowns (computed with MATLAB and rounded to the second significant digit) is given by
Thus, page 4 is the most important one. It is possible to multiply the solution, i.e., the importance values
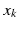
, by a positive constant. Such a multiplication or scaling is often advantageous for computational methods or for the visual display of the results. For example, the scaling could be used to give the most important page the value 1.00. A scaling is allowed, since it does not change the ranking of the pages, which is the essential information provided by the PageRank algorithm.
1.2 No Claim Discounting in Car Insurances
Insurance companies compute the premiums for their customers on the basis of the insured risk: the higher the risk, the higher the premium. It is therefore important to identify the factors that lead to higher risk. In the case of a car insurance these factors include the number of miles driven per year, the distance between home and work, the marital status, the engine power, or the age of the driver. Using such information, the company calculates the initial premium.
Usually the best indicator for future accidents, and hence future insurance claims, is the number of accidents of the individual customer in the past, i.e., the claims history. In order to incorporate this information into the premium rates, insurers establish a system of risk classes , which divide the customers into homogeneous risk groups with respect to their previous claims history. Customers with fewer accidents in the past get a discount on their premium. This approach is called a no claims discounting scheme .
For a mathematical model of this scheme we need a set of risk classes and a transition rule for moving between the classes. At the end of a policy year, the customer may move to a different class depending on the claims made during the year. The discount is given in percent of the premium in the initial class. As a simple example we consider four risk classes,
and the following transition rules:
No accident: Step up one class (or stay in
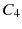
).
One accident: Step back one class (or stay in
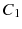
).
More than one accident: Step back to class
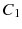













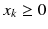 . A page k is more important than a page j if
. A page k is more important than a page j if 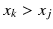 . If a page k has a link to a page j , we say that page j has a backlink from page k . In the above description these backlinks are the votes. As an example, consider the following link structure:
. If a page k has a link to a page j , we say that page j has a backlink from page k . In the above description these backlinks are the votes. As an example, consider the following link structure: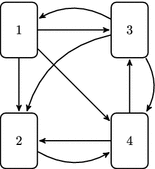
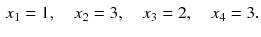
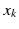 as the sum of all importance values of the backlinks of the page k . In our example this results in four equations that have to be satisfied simultaneously,
as the sum of all importance values of the backlinks of the page k . In our example this results in four equations that have to be satisfied simultaneously, 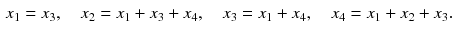
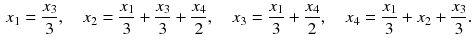
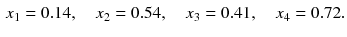
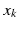 , by a positive constant. Such a multiplication or scaling is often advantageous for computational methods or for the visual display of the results. For example, the scaling could be used to give the most important page the value 1.00. A scaling is allowed, since it does not change the ranking of the pages, which is the essential information provided by the PageRank algorithm.
, by a positive constant. Such a multiplication or scaling is often advantageous for computational methods or for the visual display of the results. For example, the scaling could be used to give the most important page the value 1.00. A scaling is allowed, since it does not change the ranking of the pages, which is the essential information provided by the PageRank algorithm.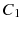
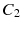
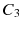
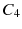
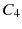 ).
).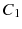 ).
).