Ferrante Neri - Linear Algebra for Computational Sciences and Engineering

The history of linear algebra can be viewed within the context of two important traditions.

The first tradition (within the history of mathematics) consists of the progressive broadening of the concept of number so to include not only positive integers but also negative numbers, fractions and algebraic and transcendental irrationals. Moreover, the symbols in the equations became matrices, polynomials, sets and, permutations. Complex numbers and vector analysis belong to this tradition. Within the development of mathematics, the one was concerned not so much about solving specific equations but mostly about addressing general and fundamental questions. The latter were approached by extending the operations and the properties of sum and multiplication from integers to other linear algebraic structures. Different algebraic structures (lattices and Boolean algebra) generalized other kinds of operations, thus allowing to optimize some non-linear mathematical problems. As a first example, lattices were generalizations of order relations on algebraic spaces, such as set inclusion in set theory and inequality in the familiar number systems ( 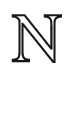, , , 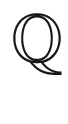and 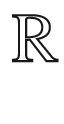). As a second example, Boolean algebra generalized the operations of intersection and union and the principle of duality (De Morgans relations), already valid in set theory, to formalize the logic and the propositions calculus. This approach to logic as an algebraic structure was much similar as the Descartes algebra approach to the geometry. Set theory and logic have been further advanced in the past centuries. In particular, Hilbert attempted to build up mathematics by using symbolic logic in a way that could prove its consistency. On the other hand, Gdel proved that in any mathematical system, there will always be statements that can never be proven either true or false.

The second tradition (within the history of physical science) consists of the search for mathematical entities and operations that represent aspects of the physical reality. This tradition played a role in the Greek geometrys bearing and its following application to physical problems. When observing the space around us, we always suppose the existence of a reference frame, identified with an ideal rigid body, in the part of the universe in which the system we want to study evolves (e.g. a three axes system having the sun as their origin and direct versus three fixed stars). This is modelled in the so-called Euclidean affine space. A reference frames choice is purely descriptive at a purely kinematic level. Two reference frames have to be intuitively considered distinct if the correspondent rigid bodies are in relative motion. Therefore, it is important to fix the links ( linear transformations ) between the kinematic entities associated with the same motion but relatives to two different reference frames ( Galileos relativity ).

In the seventeenth and eighteenth centuries, some physical entities needed a new representation. This necessity made the above-mentioned two traditions converge by adding quantities as velocity, force, momentum and acceleration ( vectors ) to the traditional quantities as mass and time ( scalars ). Important ideas led to the vectors major systems: the forces parallelogram concept by Galileo, the situations geometry and calculus concepts by Leibniz and by Newton and the complex numbers geometrical representation. Kinematics studies the motion of bodies in space and in time independently on the causes which provoke it. In classical physics, the role of time is reduced to that of a parametric independent variable. It needs also to choose a model for the body (or bodies) whose motion one wants to study. The fundamental and simpler model is that of point (useful only if the bodys extension is smaller than the extension of its motion and of the other important physical quantities considered in a particular problem). The motion of a point is represented by a curve in the tridimensional Euclidean affine space. A second fundamental model is the rigid body one, adopted for those extended bodies whose component particles do not change mutual distances during the motion.

Later developments in electricity, magnetism and optics further promoted the use of vectors in mathematical physics. The nineteenth century marked the development of vector space methods, whose prototypes were the three-dimensional geometric extensive algebra by Grassmann and the algebra of quaternions by Hamilton to, respectively, represent the orientation and rotation of a body in three dimensions. Thus, it was already clear how a simple algebra should meet the needs of the physicists in order to efficiently describe objects in space and in time (in particular their dynamical symmetries and the corresponding conservation laws) and the properties of space-time itself. Furthermore, the principal characteristic of a simple algebra had to be its linearity (or at most its multi-linearity). During the latter part of the nineteenth century, Gibbs based his three-dimensional vector algebra on some ideas by Grassmann and by Hamilton, while Clifford united these systems into a single geometric algebra (direct product of quaternions algebras). Afterwards, the Einsteins description of the four-dimensional continuum space-time (special and general relativity theories) required a tensor algebra. In the 1930s, Pauli and Dirac introduced Clifford algebras matrix representations for physical reasons: Pauli for describing the electron spin while Dirac for accommodating both the electron spin and the special relativity.