1.1 Introduction
This book emphasizes the use of polynomials, and more generally, rational functions, as the vehicle for the development of linear algebra and linear system theory. This is a powerful and elegant idea, and the development of linear theory is leaning more toward the conceptual than toward the technical. However, this approach has its own weakness. The stumbling block is that before learning linear algebra, one has to know the basics of algebra. Thus groups, rings, fields, and modules have to be introduced. This we proceed to do, accompanied by some examples that are relevant to the content of the rest of the book.
1.2 Sets and Maps
Let S be a set. If between elements of the set a relation a b is defined, so that either a b holds or not, then we say we have a binary relation . If a binary relation in S satisfies the following conditions:
a a holds for all a S
a b b a
a b and b c a c
then we say we have an equivalence relation in S . The three conditions are referred to as reflexivity, symmetry, and transitivity respectively.
For each a S we define its equivalence class by S a ={ x S x a }. Clearly S a S and S a . An equivalence relation leads to a partition of the set S . By a partition of S we mean a representation of S as the disjoint union of subsets. Since clearly, using transitivity, either S a S b = or S a = S b , and S = a S S a , the set of equivalence classes is a partition of S . Similarly, any partition S = S defines an equivalence relation by letting a b if for some we have a , b S .
A rule that assigns to each member a A a unique member b B is called a map or a function from A into B . We will denote this by f : A B or A { f \atop } B . We denote by f ( A ) the image of the set A defined by
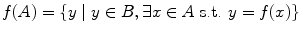
. The inverse image of a subset M B is defined by
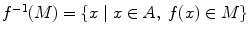
. A map f : A B is called injective or 1-to-1 if f ( x )= f ( y ) implies x = y . A map f : A B is called surjective or onto if f ( A )= B , i.e., for each y B there exists an x A such that y = f ( x ). A map f is called bijective if it is both injective and surjective.
Given maps f : A B and g : B C , we can define a map h : A C by letting h ( x )= g ( f ( x )). We call this map h the composition or product of the maps f and g . This will be denoted by h = g f . Given three maps A { f \atop } B { g \atop } C { h \atop } D , we compute h ( g f )( x )= h ( g ( f ( x ))) and ( h g ) f ( x )= h ( g ( f ( x ))). So the product of maps is associative, i.e.,
Due to the associative law of composition, we can write h g f , and more generally f n f 1, unambiguously.
Given a map f : A B , we define an equivalence relationin A by letting
Thus the equivalence class of a is given by
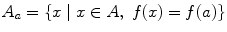
. We will denote by A the set of equivalence classes and refer to this as the quotient set by the equivalence relation.
Next we define three transformations
with the f i defined by
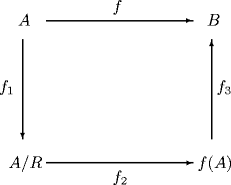
Clearly the map f 1 is surjective, f 2 is bijective and f 3 injective. Moreover, we have f = f 3 f 2 f 1. This factorization of f is referred to as the canonical factorization . The canonical factorization can be described also via the following commutative diagram:
We note that f 2 f 1 is surjective, whereas f 3 f 2 is injective.
1.3 Groups
Given a set M , a binary operation in M is a map from M M into M . Thus, an ordered pair ( a , b ) is mapped into an element of M denoted by ab . A set M with an associative binary operation is called a semigroup. Thus if a , b M we have ab M , and the associative rule a ( bc )=( ab ) c holds. Thus the product a 1 a n of elements of M is unambiguously defined.
We proceed to define the notion of a group, which is the cornerstone of most mathematical structures.
Definition 1.1.
A group is a set G with a binary operation, called multiplication, that satisfies
a ( bc )=( ab ) c , i.e., the associative law.
There exists a left identity, or unit element, e G , i.e., ea = a for all a G .
For each a G there exists a left inverse, denoted by a 1, which satisfies
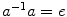
.
A group G is called abelian if the group operation is commutative, i.e., if ab = ba holds for all a , b G .
In many cases, an abelian group operation will be denoted using the additive notation, i.e., a + b rather than ab , as in the case of the group of integers
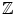
with addition as the group operation. Other useful examples are
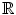
, the set of all real numbers under addition, and
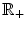
, the set of all positive real numbers with multiplication as the group operation.
Given a nonempty set S , the set of all bijective mappings of S onto itself forms a group with the group action being composition. The elements of G are called permutations of S . If S ={ 1,, n }, then the group of permutations of S is called the symmetric group of degree n and denoted by S n .
Theorem 1.2.
Let G be a group and let a be an element of G. Then a left inverse a 1 of a is also a right inverse.
A left identity is also a right identity .
The identity element of a group is unique.











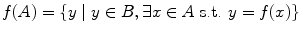 . The inverse image of a subset M B is defined by
. The inverse image of a subset M B is defined by 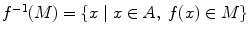 . A map f : A B is called injective or 1-to-1 if f ( x )= f ( y ) implies x = y . A map f : A B is called surjective or onto if f ( A )= B , i.e., for each y B there exists an x A such that y = f ( x ). A map f is called bijective if it is both injective and surjective.
. A map f : A B is called injective or 1-to-1 if f ( x )= f ( y ) implies x = y . A map f : A B is called surjective or onto if f ( A )= B , i.e., for each y B there exists an x A such that y = f ( x ). A map f is called bijective if it is both injective and surjective.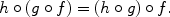
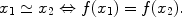
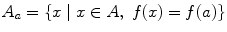 . We will denote by A the set of equivalence classes and refer to this as the quotient set by the equivalence relation.
. We will denote by A the set of equivalence classes and refer to this as the quotient set by the equivalence relation.
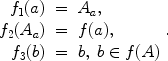
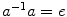 .
.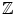 with addition as the group operation. Other useful examples are
with addition as the group operation. Other useful examples are 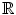 , the set of all real numbers under addition, and
, the set of all real numbers under addition, and 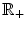 , the set of all positive real numbers with multiplication as the group operation.
, the set of all positive real numbers with multiplication as the group operation.