1. Introduction
This chapter provides a preview of the book but is presented in a rather abstract setting and will be easier to follow after reading the rest of the book. The reader may omit this chapter on first reading and refer back to it as necessary. Chapters illustrates some of these extensions for the generalized linear model (GLM) and the generalized additive model (GAM).
Response variables are the variables of interest, and are predicted with a p 1 vector of predictor variables x =( x 1,, x p ) T where x T is the transpose of x . A multivariate regression model has m >1 response variables. For example, predict Y 1= systolic blood pressure and Y 2= diastolic blood pressure using a constant x 1, x 2= age , x 3= weight , and x 4= dosage amount of blood pressure medicine . The multivariate location and dispersion model of Chapter .
A univariate regression model has one response variable Y . Suppose Y is independent of the predictor variables x given a function h ( x ), written
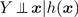
, where

and the integer d is as small as possible. Then Y follows a dD regression model, where d p since
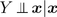
. If
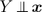
, then Y follows a 0 D regression model. Then there are 0D, 1D, , pD regression models, and all univariate regression models are dD regression models for some integer 0 d p . Cook (, p. 414) use similar notation with
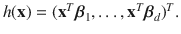
The remainder of this chapter considers 1D regression models, where
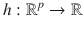
is a real function. The additive error regression model Y = m ( x ) + e is an important special case with h ( x )= m ( x ).See Section An important special case of the additive error model is the linear regression model
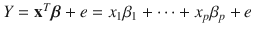
. Multiple linear regression and many experimental design models are special cases of the linear regression model.
The multiple linear regression model has at least one predictor x i that takes on many values. Chapter consider response plots, plots for response transformations, and prediction intervals for the multiple linear regression model fit by least squares. All of these techniques can be extended to alternative fitting methods.
1.1 Some Regression Models
All models are wrong, but some are useful.
Box ()
In data analysis , an investigator is presented with a problem and data from some population . The population might be the collection of all possible outcomes from an experiment while the problem might be predicting a future value of the response variable Y or summarizing the relationship between Y and the p 1 vector of predictor variables x .A statistical model is used to provide a useful approximation to some of the important underlying characteristics of the population which generated the data. Many of the most used models for 1D regression, defined below, are families of conditional distributions Y | x = x o indexed by x = x o . A 1D regression model is a parametric model if the conditional distribution is completely specified except for a fixed finite number of parameters, otherwise, the 1D model is a semiparametric model . GLMs and GAMs, defined below, are covered in Chapter .
Definition 1.1.
Regression investigates how the response variable Y changes with the value of a p 1 vector x of predictors. Often this conditional distribution Y | x is described by a 1D regression model , where Y is conditionally independent of x given the sufficient predictor SP = h ( x ), written
where the real valued function
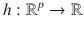
. The estimated sufficient predictor ESP =
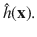
An important special case is a model with a linear predictor
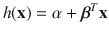
where ESP =
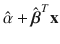
. This class of models includes the generalized linear model (GLM). Another important special case is a generalized additive model (GAM), where Y is independent of x =( x 1,, x p ) T given the additive predictor AP = + j =1 p S j ( x j ) for some (usually unknown) functions S j . The estimated additive predictor EAP = ESP =
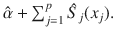
Notation: In this text, a plot of x versus Y will have x on the horizontal axis, and Y on the vertical axis.
Plots are extremely important for regression. When p =1, x is both a sufficient predictor and an estimated sufficient predictor. So a plot of x versus Y is both a sufficient summary plot and a response plot. Usually the SP is unknown, so only the response plot can be made. The response plot will be extremely useful for checking the goodness of fit of the 1D regression model.
Definition 1.2.
A sufficient summary plot is a plot of the SP versus Y . An estimated sufficient summary plot (ESSP) or response plot is a plot of the ESP versus Y .
Notation.
Often the index i will be suppressed. For example, the linear regression model
for i =1,, n where
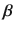
is a p 1 unknown vector of parameters, and e i is a random error. This model could be written
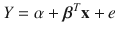
. More accurately,
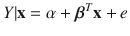
, but the conditioning on x will often be suppressed. Often the errors e 1,, e n are iid (independent and identically distributed) from a distribution that is known except for a scale parameter. For example, the e i s might be iid from a normal (Gaussian) distribution with mean 0 and unknown standard deviation .For this Gaussian model, estimation of ,
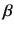
, and is important for inference and for predicting a new value of the response variable Y f given a new vector of predictors x f .
The class of 1D regression models is very rich, and many of the most used statistical models, including GLMs and GAMs, are 1D regression models. Nonlinear regression, nonparametric regression, and linear regression are special cases of the additive error regression model













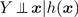 , where
, where  and the integer d is as small as possible. Then Y follows a dD regression model, where d p since
and the integer d is as small as possible. Then Y follows a dD regression model, where d p since 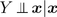 . If
. If 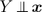 , then Y follows a 0 D regression model. Then there are 0D, 1D, , pD regression models, and all univariate regression models are dD regression models for some integer 0 d p . Cook (, p. 414) use similar notation with
, then Y follows a 0 D regression model. Then there are 0D, 1D, , pD regression models, and all univariate regression models are dD regression models for some integer 0 d p . Cook (, p. 414) use similar notation with 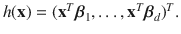
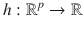 is a real function. The additive error regression model Y = m ( x ) + e is an important special case with h ( x )= m ( x ).See Section An important special case of the additive error model is the linear regression model
is a real function. The additive error regression model Y = m ( x ) + e is an important special case with h ( x )= m ( x ).See Section An important special case of the additive error model is the linear regression model 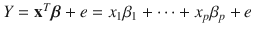 . Multiple linear regression and many experimental design models are special cases of the linear regression model.
. Multiple linear regression and many experimental design models are special cases of the linear regression model.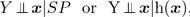
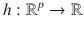 . The estimated sufficient predictor ESP =
. The estimated sufficient predictor ESP = 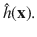 An important special case is a model with a linear predictor
An important special case is a model with a linear predictor 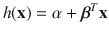 where ESP =
where ESP = 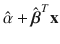 . This class of models includes the generalized linear model (GLM). Another important special case is a generalized additive model (GAM), where Y is independent of x =( x 1,, x p ) T given the additive predictor AP = + j =1 p S j ( x j ) for some (usually unknown) functions S j . The estimated additive predictor EAP = ESP =
. This class of models includes the generalized linear model (GLM). Another important special case is a generalized additive model (GAM), where Y is independent of x =( x 1,, x p ) T given the additive predictor AP = + j =1 p S j ( x j ) for some (usually unknown) functions S j . The estimated additive predictor EAP = ESP = 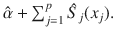
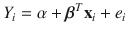
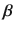 is a p 1 unknown vector of parameters, and e i is a random error. This model could be written
is a p 1 unknown vector of parameters, and e i is a random error. This model could be written 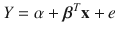 . More accurately,
. More accurately, 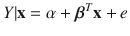 , but the conditioning on x will often be suppressed. Often the errors e 1,, e n are iid (independent and identically distributed) from a distribution that is known except for a scale parameter. For example, the e i s might be iid from a normal (Gaussian) distribution with mean 0 and unknown standard deviation .For this Gaussian model, estimation of ,
, but the conditioning on x will often be suppressed. Often the errors e 1,, e n are iid (independent and identically distributed) from a distribution that is known except for a scale parameter. For example, the e i s might be iid from a normal (Gaussian) distribution with mean 0 and unknown standard deviation .For this Gaussian model, estimation of , 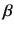 , and is important for inference and for predicting a new value of the response variable Y f given a new vector of predictors x f .
, and is important for inference and for predicting a new value of the response variable Y f given a new vector of predictors x f .