1. Prediction: Some Heuristic Notions
1.1 To Explain or to Predict?
Statistics is the scientific discipline that enables us to draw inferences about the real world on the basis of observed data. Statistical inference comes in two general flavors:
A.
Explaining/modeling the world . Here the role of the statistician is much like the role of a natural scientist trying to find how the observed/observable quantity Y depends on another observed/observable quantity X . Natural scientists may have additional information at their disposal, e.g., physical laws of conservation, etc., but the statistician must typically answer this question solely on the basis of the data at hand. Nonetheless, insights provided by the science behind the data can help the statistician formulate a better model.
In a question asked this way, Y is called the response variable, and X is called a regressor or predictor variable. The data are often pairs:
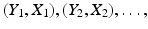
( Y n , X n ), where Y i is the measured response associated with a regressor value given by X i . Figure a shows an example of a scatterplot associated with such a dataset.
The goal is to find a so-called regression function, say (), such that Y ( X ). The relation Y ( X ) is written as an approximation because either the association between X and Y is not exact and/or the observation of X and Y is corrupted by measurement error. The inexactness of the association and the possible measurement errors are combined in the discrepancy defined as
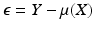
; the last equation can then be re-written as:
In the above, ( X ) is the part of Y that is explainable by X , and is an unexplainable, error term.
Is Eq.().
In addition to assumptions on the error term , typical model assumptions specify the allowed type for function (). This is done by specifying a family of functions, say
and insisting that () must belong to
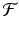
. If
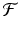
is finite-dimensional, then it is called a parametric family. A popular two-dimensional example corresponds to
which is the usual straight-line regression with slope 1 and intercept 0. If
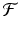
is not finite-dimensional, then it is called a nonparametric (sometimes also called infinite-parametric) family. For instance,
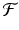
could be the family of all functions that are (say) twice continuously differentiable over their support.
Under such model assumptions, the task of the statistician is to use the available data
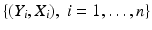
in order to (a) optimally estimate the function
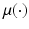
, and (b) to quantify the statistical/stochastic accuracy of the estimator.
Part (a) can be accomplished after formulating an appropriate optimality criterion; the oldest and most popular such criterion is Least Squares (LS) . The LS estimator of
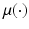
is the function, say
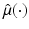
, that minimizes the sum of squared errors
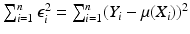
among all
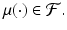
If
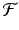
happens to be the two-parameter family of straight-line regression functions, then it is sufficient to obtain LS estimates, say
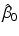
and
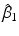
, of the intercept and slope 0 and 1, respectively. Under a correctly specified model, the LS estimators
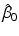
and
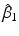
have minimum variance among all unbiased estimators that are linear functions of the data.
To address part (b) before the 1980s statisticians often resorted to further restrictive model assumptions such as an (exact) Gaussian distribution for the errors i . Fortunately, the bootstrap and other computer-intensive methods have rendered such unrealistic/unverifiable assumptions obsolete; see, e.g., Efron ().
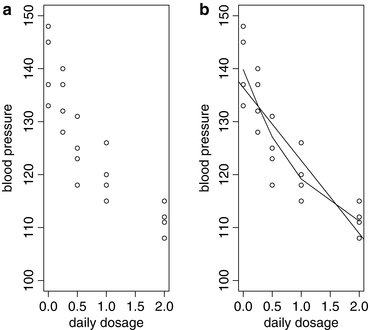
To fix ideas, consider a toy example involving n =20 patients taken from a group of people with borderline high blood pressure, i.e., (systolic) blood pressure of about 140. A drug for lowering blood pressure may be under consideration, and the question is to empirically see how (systolic) blood pressure Y corresponds to dosage X where the latter is measured as units of the drug taken daily. The Y responses were as follows: (145,148,133,137) for X =0; (140,132,137,128) for X =0.25; (123,131,118,125) for X =0.5; (115,118,120,126) for X =1; and (108,115,111,112) for X =2. Figure b shows the scatterplot of the 20 data pairs ( Y i , X i ), one for each patient, having superimposed both the LS straight-line regression function (with estimated intercept and slope equal to 136.5 and 13.7, respectively), as well as an estimated nonparametric regression function based on a smoothing spline, i.e., piecewise cubic function, under the assumption that the true function () is smooth, e.g., twice continuously differentiable.
Fig. 1.1
( a ) Systolic blood pressure vs. daily dosage of a drug. ( b ) Same data with superimposed straight-line regression as well as nonparametric regression based on a smoothing spline













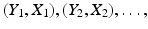 ( Y n , X n ), where Y i is the measured response associated with a regressor value given by X i . Figure a shows an example of a scatterplot associated with such a dataset.
( Y n , X n ), where Y i is the measured response associated with a regressor value given by X i . Figure a shows an example of a scatterplot associated with such a dataset.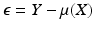 ; the last equation can then be re-written as:
; the last equation can then be re-written as: 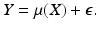
 and insisting that () must belong to
and insisting that () must belong to  . If
. If 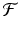 is finite-dimensional, then it is called a parametric family. A popular two-dimensional example corresponds to
is finite-dimensional, then it is called a parametric family. A popular two-dimensional example corresponds to 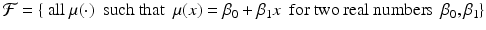
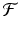 is not finite-dimensional, then it is called a nonparametric (sometimes also called infinite-parametric) family. For instance,
is not finite-dimensional, then it is called a nonparametric (sometimes also called infinite-parametric) family. For instance, 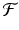 could be the family of all functions that are (say) twice continuously differentiable over their support.
could be the family of all functions that are (say) twice continuously differentiable over their support.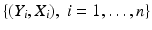 in order to (a) optimally estimate the function
in order to (a) optimally estimate the function 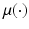 , and (b) to quantify the statistical/stochastic accuracy of the estimator.
, and (b) to quantify the statistical/stochastic accuracy of the estimator.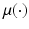 is the function, say
is the function, say 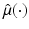 , that minimizes the sum of squared errors
, that minimizes the sum of squared errors 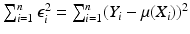 among all
among all 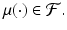 If
If 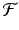 happens to be the two-parameter family of straight-line regression functions, then it is sufficient to obtain LS estimates, say
happens to be the two-parameter family of straight-line regression functions, then it is sufficient to obtain LS estimates, say  and
and 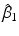 , of the intercept and slope 0 and 1, respectively. Under a correctly specified model, the LS estimators
, of the intercept and slope 0 and 1, respectively. Under a correctly specified model, the LS estimators 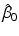 and
and 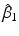 have minimum variance among all unbiased estimators that are linear functions of the data.
have minimum variance among all unbiased estimators that are linear functions of the data.