Ayyadevara - Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R
Here you can read online Ayyadevara - Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Berkeley;CA, year: 2018, publisher: Apress, genre: Computer. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R
- Author:
- Publisher:Apress
- Genre:
- Year:2018
- City:Berkeley;CA
- Rating:4 / 5
- Favourites:Add to favourites
- Your mark:
Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Chapter 1: Basics of Machine Learning -- Chapter 2: Linear regression -- Chapter 3: Logistic regression -- Chapter 4: Decision tree -- Chapter 5: Random forest -- Chapter 6: GBM -- Chapter 7: Neural network -- Chapter 8: word2vec -- Chapter 9: Convolutional neural network -- Chapter 10: Recurrent Neural Network -- Chapter 11: Clustering -- Chapter 12: PCA -- Chapter 13: Recommender systems -- Chapter 14: Implementing algorithms in the cloud.;Bridge the gap between a high-level understanding of how an algorithm works and knowing the nuts and bolts to tune your models better. This book will give you the confidence and skills when developing all the major machine learning models. In Pro Machine Learning Algorithms, you will first develop the algorithm in Excel so that you get a practical understanding of all the levers that can be tuned in a model, before implementing the models in Python/R. You will cover all the major algorithms: supervised and unsupervised learning, which include linear/logistic regression; k-means clustering; PCA; recommender system; decision tree; random forest; GBM; and neural networks. You will also be exposed to the latest in deep learning through CNNs, RNNs, and word2vec for text mining. You will be learning not only the algorithms, but also the concepts of feature engineering to maximize the performance of a model. You will see the theory along with case studies, such as sentiment classification, fraud detection, recommender systems, and image recognition, so that you get the best of both theory and practice for the vast majority of the machine learning algorithms used in industry. Along with learning the algorithms, you will also be exposed to running machine-learning models on all the major cloud service providers. You are expected to have minimal knowledge of statistics/software programming and by the end of this book you should be able to work on a machine learning project with confidence. You will: Get an in-depth understanding of all the major machine learning and deep learning algorithms Fully appreciate the pitfalls to avoid while building models Implement machine learning algorithms in the cloud Follow a hands-on approach through case studies for each algorithm Gain the tricks of ensemble learning to build more accurate models Discover the basics of programming in R/Python and the Keras framework for deep learning.
Ayyadevara: author's other books
Who wrote Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R? Find out the surname, the name of the author of the book and a list of all author's works by series.
Kolla Bhanu Prakash (editor)
Miller
Dimitris N. Politis
Kaushal Gyandeep
Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
V Kishore Ayyadevara 2018
V Kishore Ayyadevara Pro Machine Learning Algorithms1. Basics of Machine Learning
V Kishore Ayyadevara 1
(1)
Hyderabad, Andhra Pradesh, India
Machine learning can be broadly classified into supervised and unsupervised learning. By definition, the term supervised means that the machine (the system) learns with the help of somethingtypically a labeled training data.
Training data (or a dataset ) is the basis on which the system learns to infer. An example of this process is to show the system a set of images of cats and dogs with the corresponding labels of the images (the labels say whether the image is of a cat or a dog) and let the system decipher the features of cats and dogs.
Similarly, unsupervised learning is the process of grouping data into similar categories. An example of this is to input into the system a set of images of dogs and cats without mentioning which image belongs to which category and let the system group the two types of images into different buckets based on the similarity of images.
In this chapter, we will go through the following:
- The difference between regression and classification
- The need for training, validation, and testing data
- The different measures of accuracy
Regression and Classification
Lets assume that we are forecasting for the number of units of Coke that would be sold in summer in a certain region. The value ranges between certain valueslets say 1 million to 1.2 million units per week. Typically, regression is a way of forecasting for such continuous variables.
Classification or prediction , on the other hand, predicts for events that have few distinct outcomesfor example, whether a day will be sunny or rainy.
Linear regression is a typical example of a technique to forecast continuous variables, whereas logistic regression is a typical technique to predict discrete variables. There are a host of other techniques, including decision trees, random forests, GBM, neural networks, and more, that can help predict both continuous and discrete outcomes.
Training and Testing Data
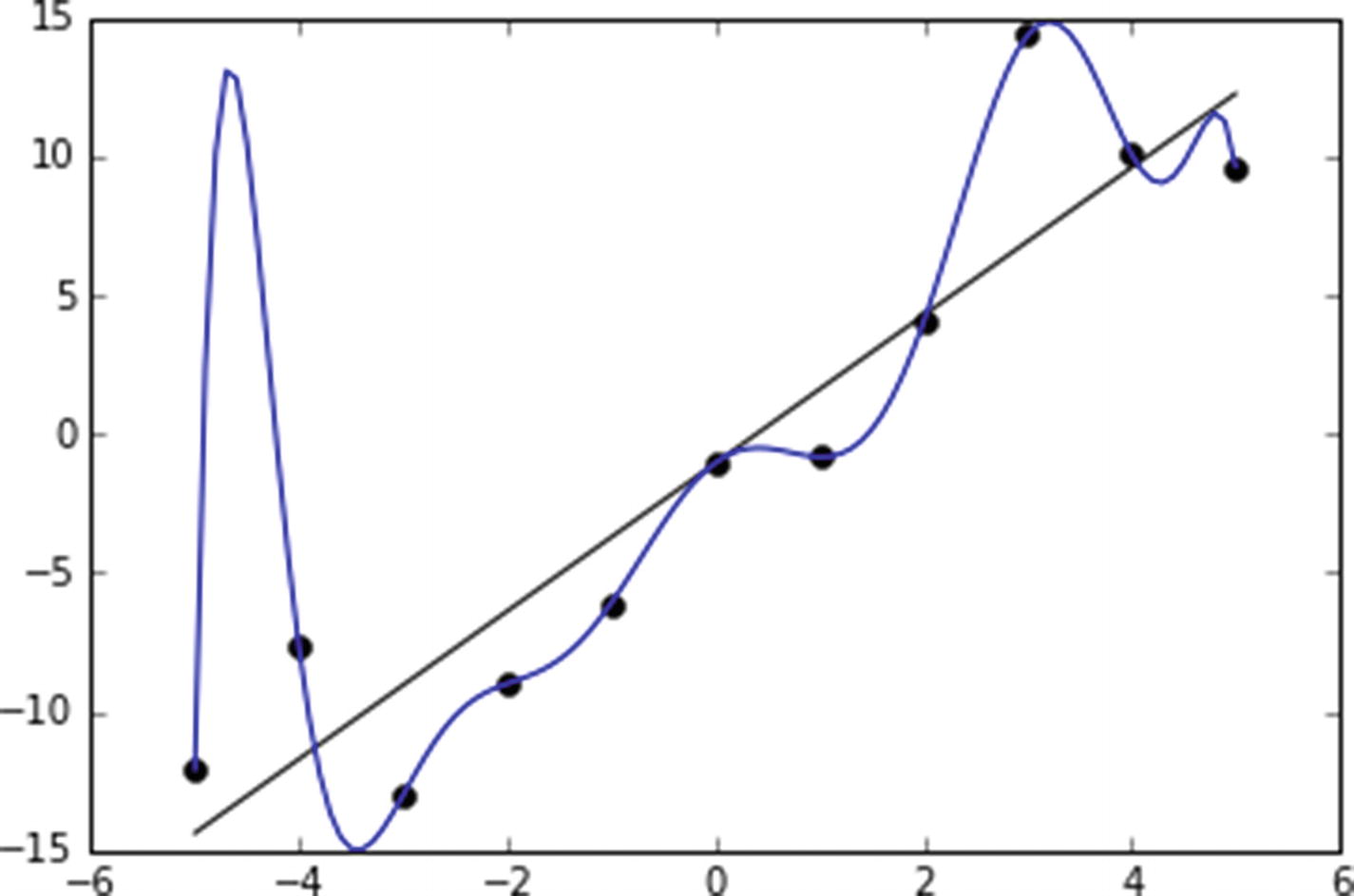
Typically, in regression, we deal with the problem of generalization/overfitting. Overfitting problems arise when the model is so complex that it perfectly fits all the data points, resulting in a minimal possible error rate. A typical example of an overfitted dataset looks like Figure . 
Figure 1-1
An overfitted dataset
From the dataset in the figure, you can see that the straight line does not fit all the data points perfectly, whereas the curved line fits the points perfectlyhence the curve has minimal error on the data points on which it is trained.
However, the straight line has a better chance of being more generalizable when compared to the curve on a new dataset. So, in practice, regression/classification is a trade-off between the generalizability of the model and complexity of model.
The lower the generalizability of the model , the higher the error rate will be on unseen data points.
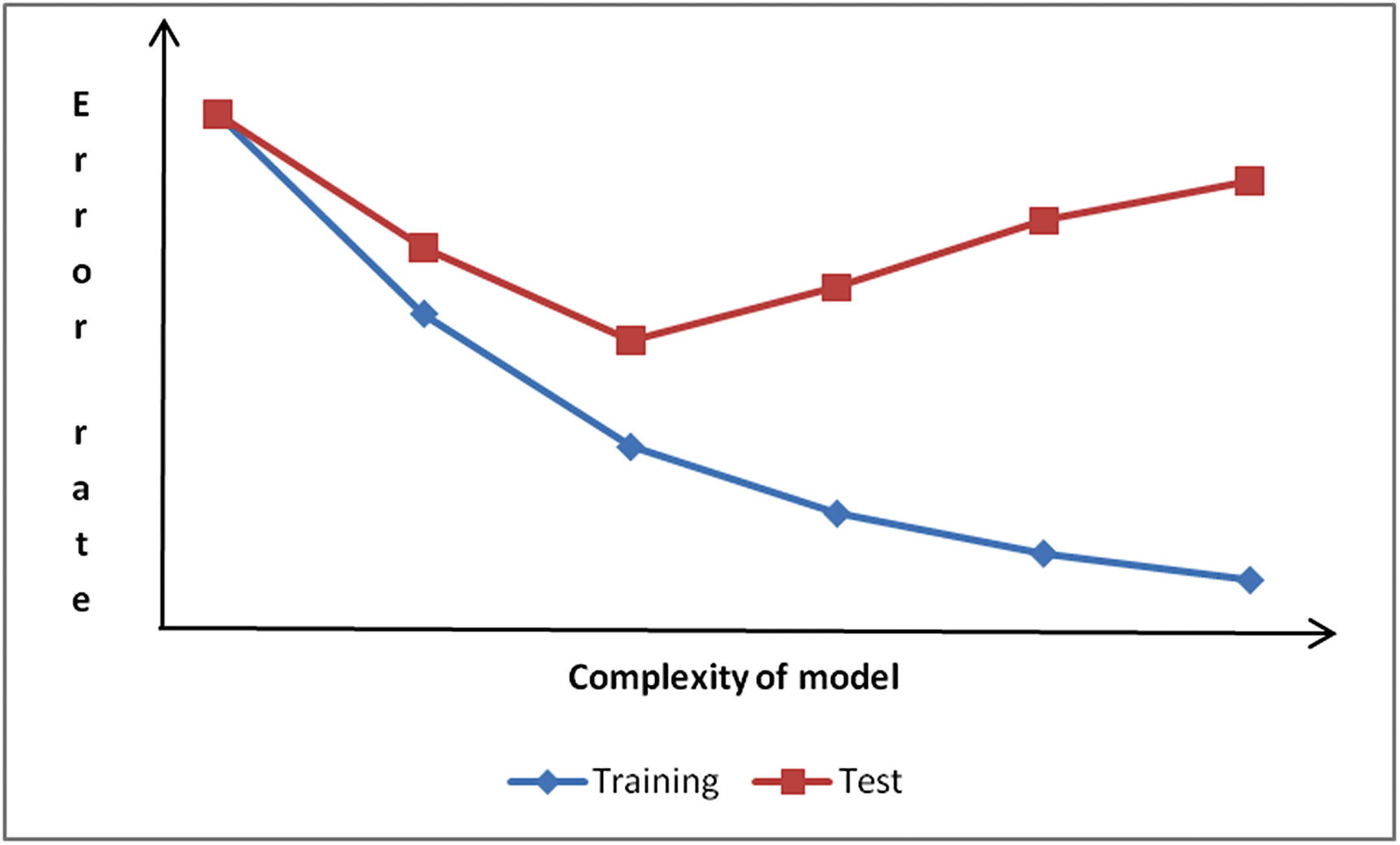
This phenomenon can be observed in Figure . As the complexity of the model increases, the error rate of unseen data points keeps reducing up to a point, after which it starts increasing again. However, the error rate on training dataset keeps on decreasing as the complexity of model increases - eventually leading to overfitting. 
Figure 1-2
Error rate in unseen data points
The unseen data points are the points that are not used in training the model, but are used in testing the accuracy of the model, and so are called testing data or test data .
The Need for Validation Dataset
The major problem in having a fixed training and testing dataset is that the test dataset might be very similar to the training dataset, whereas a new (future) dataset might not be very similar to the training dataset. The result of a future dataset not being similar to a training dataset is that the models accuracy for the future dataset may be very low.
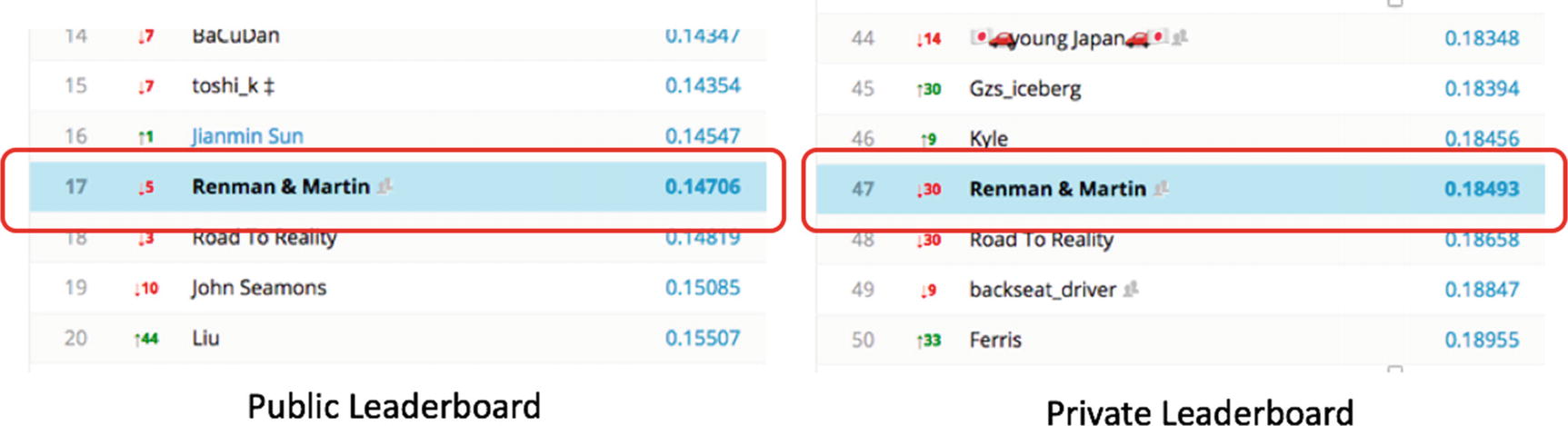
An intuition of the problem is typically seen in data science competitions and hackathons like Kaggle ( www.kaggle.com ). The public leaderboard is not always the same as the private leaderboard. Typically, for a test dataset, the competition organizer will not tell the users which rows of the test dataset belong to the public leaderboard and which belong to the private leaderboard. Essentially, a randomly selected subset of test dataset goes to the public leaderboard and the rest goes to the private leaderboard.
One can think of the private leaderboard as a test dataset for which the accuracy is not known to the user, whereas with the public leaderboard the user is told the accuracy of the model .
Potentially, people overfit on the basis of the public leaderboard, and the private leaderboard might be a slightly different dataset that is not highly representative of the public leaderboards dataset .
The problem can be seen in Figure . 
Figure 1-3
The problem illustrated
In this case, you would notice that a user moved down from rank 17 to rank 47 when compared between public and private leaderboards. Cross-validation is a technique that helps avoid the problem. Lets go through the workings in detail.
If we only have a training and testing dataset, given that the testing dataset would be unseen by the model, we would not be in a position to come up with the combination of hyper-parameters (A hyper-parameter can be thought of as a knob that we change to improve our models accuracy) that maximize the models accuracy on unseen data unless we have a third dataset. Validation is the third dataset that can be used to see how accurate the model is when the hyper-parameters are changed. Typically, out of the 100% data points in a dataset, 60% are used for training, 20% are used for validation, and the remaining 20% are for testing the dataset.
Another idea for a validation dataset goes like this: assume that you are building a model to predict whether a customer is likely to churn in the next two months. Most of the dataset will be used to train the model, and the rest can be used to test the dataset. But in most of the techniques we will deal with in subsequent chapters, youll notice that they involve hyper-parameters.
As we keep changing the hyper-parameters, the accuracy of a model varies by quite a bit, but unless there is another dataset, we cannot ascertain whether accuracy is improving. Heres why:
- We cannot test a models accuracy on the dataset on which it is trained.
- We cannot use the result of test dataset accuracy to finalize the ideal hyper-parameters, because, practically, the test dataset is unseen by the model.
Hence, the need for a third datasetthe validation dataset .
Measures of Accuracy
In a typical linear regression (where continuous values are predicted), there are a couple of ways of measuring the error of a model. Typically, error is measured on the testing dataset, because measuring error on the training dataset (the dataset a model is built on) is misleadingas the model has already seen the data points, and we would not be in a position to say anything about the accuracy on a future dataset if we test the models accuracy on the training dataset only. Thats why error is always measured on the dataset that is not used to build a model.
Light
Font size:
↓
↑
Reset
Interval:
↓
↑
Bookmark:
Make
Similar books «Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R»
Look at similar books to Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
Kolla Bhanu Prakash (editor)
Miller
Dimitris N. Politis
Kaushal Gyandeep
Reviews about «Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R»
Discussion, reviews of the book Pro Machine Learning Algorithms: A Hands-On Approach to Implementing Algorithms in Python and R and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.