Robert G. Underwood - Fundamentals of Hopf Algebras
Here you can read online Robert G. Underwood - Fundamentals of Hopf Algebras full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2015, publisher: Springer, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Fundamentals of Hopf Algebras
- Author:
- Publisher:Springer
- Genre:
- Year:2015
- Rating:5 / 5
- Favourites:Add to favourites
- Your mark:
Fundamentals of Hopf Algebras: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Fundamentals of Hopf Algebras" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
This text aims to provide graduate students with a self-contained introduction to topics that are at the forefront of modern algebra, namely, coalgebras, bialgebras and Hopf algebras. The last chapter (Chapter 4) discusses several applications of Hopf algebras, some of which are further developed in the authors 2011 publication, An Introduction to Hopf Algebras. The book may be used as the main text or as a supplementary text for a graduate algebra course. Prerequisites for this text include standard material on groups, rings, modules, algebraic extension fields, finite fields and linearly recursive sequences.
The book consists of four chapters. Chapter 1 introduces algebras and coalgebras over a field K; Chapter 2 treats bialgebras; Chapter 3 discusses Hopf algebras and Chapter 4 consists of three applications of Hopf algebras. Each chapter begins with a short overview and ends with a collection of exercises which are designed to review and reinforce the material. Exercises range from straightforward applications of the theory to problems that are devised to challenge the reader. Questions for further study are provided after selected exercises. Most proofs are given in detail, though a few proofs are omitted since they are beyond the scope of this book.
Robert G. Underwood: author's other books
Who wrote Fundamentals of Hopf Algebras? Find out the surname, the name of the author of the book and a list of all author's works by series.
Fundamentals of Hopf Algebras — read online for free the complete book (whole text) full work
Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "Fundamentals of Hopf Algebras" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.
Font size:
Interval:
Bookmark:
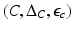as co-objects to algebras formed by reversing the arrows in the diagrams for algebras.
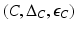is a coalgebra, then 
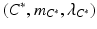is an algebra where the maps 
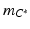and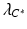 
are induced from the transposes of 
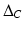and C , respectively. The converse of this statement is not true, however: if A is an algebra, then it is not always true that A is a coalgebra with structure maps induced from the transposes of the maps for A . The trick is to replace A with a certain subspace A called the finite dual (in fact, A is the largest subspace of A for which m A ( A ) A A ). Now, if A is an algebra, then A is a coalgebra. As an application we show that the finite dual K [ x ] can be identified with the collection of linearly recursive sequences of all orders over K .
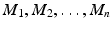as the solution to a universal mapping problem. We show that tensor products can be identified with iterated tensor products in some association.
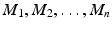be a collection of R -modules, and let A be an R -module.
,
.
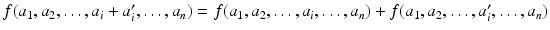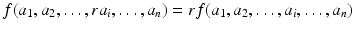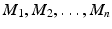over R is an R -module M 1 M 2 M n together with an R - n -linear map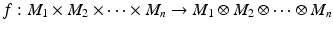 
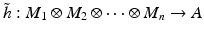for which 
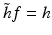, that is, the following diagram commutes.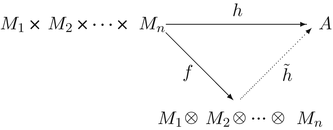
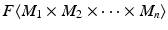denote the free R -module on the set M 1 M 2 M n . Let J be the submodule of 
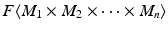generated by quantities of the form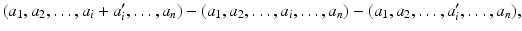 
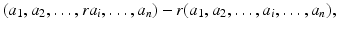
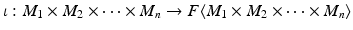
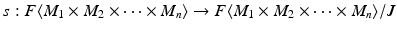
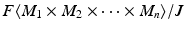together with the map f (which is clearly R - n -linear) is a tensor product; it solves the universal mapping problem described in Definition .
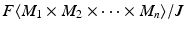together with the map f is a tensor product of 
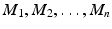over R.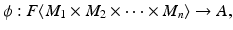
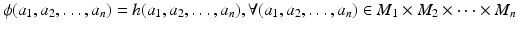. Since is R - n -linear, J ker(), and so, by the universal mapping property for kernels, there exists an R -module homomorphism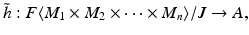 
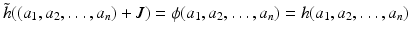. Now for all 
, 
, and so, 
Font size:
Interval:
Bookmark:
Similar books «Fundamentals of Hopf Algebras»
Look at similar books to Fundamentals of Hopf Algebras. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.
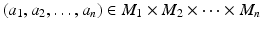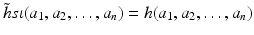Discussion, reviews of the book Fundamentals of Hopf Algebras and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.