Contents
Guide

Helmut Strade
Simple Lie Algebras over Fields of Positive Characteristic
De Gruyter Expositions in Mathematics
Edited by
Lev Birbrair, Fortaleza, Brazil
Victor P. Maslov, Moscow, Russia
Walter D. Neumann, New York City, New York, USA
Markus J. Pflaum, Boulder, Colorado, USA
Dierk Schleicher, Bremen, Germany
Volume 42

Mathematics Subject Classification 2010
17-02, 17B50, 17B20, 17B05
Author
Prof. Dr. Helmut Strade
Marmstorfer Weg 124
21077 Hamburg
Germany
ISBN 978-3-11-051676-0
e-ISBN (PDF) 978-3-11-051760-6
e-ISBN (EPUB) 978-3-11-051689-0
Set-ISBN 978-3-11-051761-3
ISSN 0938-6572
Library of Congress Cataloging-in-Publication Data
A CIP catalog record for this book has been applied for at the Library of Congress.
Bibliographic information published by the Deutsche Nationalbibliothek
The Deutsche Nationalbibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data are available on the Internet at http://dnb.dnb.de.
2017 Walter de Gruyter GmbH, Berlin/Boston
www.degruyter.com
Fr meine Shne Robert und Jrn
Introduction
This three volume monograph on Simple Lie Algebras over Fields of Positive Characteristic presents major methods on modular Lie algebras, all the examples of simple Lie algebras over algebraically closed fields of characteristic p 5 and the complete proof of the Classification Theorem mentioned in the introduction of Volume 1. The first volume contains the methods, examples and a first classification result. It turned out during the work on the reproduction of the classification proof that one has to pay for a reasonable completeness by extending the text considerably. So the whole work is now planned as a three volume monograph. This second volume contains the proof of the Classification Theorem for simple Lie algebras of absolute toral rank 2.
We have already mentioned details outlining the proof of the Classification Theorem in the introduction of the first volume. Therefore we will just recall very briefly some strategy in order to place the content of this volume into the whole picture. Already in the early work on simple Lie algebras over the complex numbers people determined, as a general procedure, 1-sections 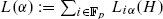 with respect to a toral CSA H , described their representations in the spaces
with respect to a toral CSA H , described their representations in the spaces 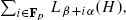 and determined 2-sections. The breakthrough paper [B-W88] made this procedure work for modular Lie algebras as well (if the characteristic is bigger than 7). It turned out, however, that the many more examples and the richness of their structures made things much more involved. Imagine that in the classical case only
and determined 2-sections. The breakthrough paper [B-W88] made this procedure work for modular Lie algebras as well (if the characteristic is bigger than 7). It turned out, however, that the many more examples and the richness of their structures made things much more involved. Imagine that in the classical case only 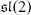 H ker occurs as the 1-section L (), while in the modular case the classical algebra
H ker occurs as the 1-section L (), while in the modular case the classical algebra 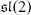 , the smallest Witt algebra W (1; ) and the smallest Hamiltonian algebra H (2; ) (2) have absolute toral rank 1 (by Corollaries 7.5.2 and 7.5.9). Hence each such algebra is a 1-section of itself. There are nonsplit radical extensions of these Cartan type Lie algebras, and it is a priori not clear which of these can occur as 1-sections of simple Lie algebras. Moreover, the representation theories of such extensions are very rich, and therefore the very details of these theories can hardly be described. Less information is, fortunately, sufficient for the Classification Theory. Namely, it is sufficient and possible to describe semisimple quotients L [] := L ()/ rad L () with respect to certain tori T (we have to decide which tori we take into consideration though), and it is also possible to describe the T -semisimple quotients of 2-sections in terms of simple Lie algebras of absolute toral rank 1 and 2 by Blocks Theorem Corollary 3.3.6. If one knows the simple Lie algebras of absolute toral rank not bigger than 2 one is able to describe all such semisimple quotients of 2-sections in these terms. In this second volume we will prove the following
, the smallest Witt algebra W (1; ) and the smallest Hamiltonian algebra H (2; ) (2) have absolute toral rank 1 (by Corollaries 7.5.2 and 7.5.9). Hence each such algebra is a 1-section of itself. There are nonsplit radical extensions of these Cartan type Lie algebras, and it is a priori not clear which of these can occur as 1-sections of simple Lie algebras. Moreover, the representation theories of such extensions are very rich, and therefore the very details of these theories can hardly be described. Less information is, fortunately, sufficient for the Classification Theory. Namely, it is sufficient and possible to describe semisimple quotients L [] := L ()/ rad L () with respect to certain tori T (we have to decide which tori we take into consideration though), and it is also possible to describe the T -semisimple quotients of 2-sections in terms of simple Lie algebras of absolute toral rank 1 and 2 by Blocks Theorem Corollary 3.3.6. If one knows the simple Lie algebras of absolute toral rank not bigger than 2 one is able to describe all such semisimple quotients of 2-sections in these terms. In this second volume we will prove the following
Theorem. Every simple Lie algebra over an algebraically closed field of characteristic p > 3 having absolute toral rank 2 is exactly one of the following:
(a) classical of type A , B or G ;
(b) the restricted Lie algebras W (2; ), S (3; ) (1) , H (4; ) (1) , K (3; ) ; the naturally graded Lie algebras W (1; ), H (2; (1, 2)) (2) ; H (2; ; ()) (1) , H (2; 1; (1)) ;
(c) the Melikian algebra 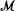 (1,1).
(1,1).
Since we classified the simple Lie algebras of absolute toral rank 1 in Chapter 9 of Volume 1, the result of this second volume will provide sufficient information on the 2-sections of simple Lie algebras with respect to adequate tori.
The proof of the Classification Theorem for simple Lie algebras of absolute toral rank 2 is completely different from what we have done in Chapter 9 of Volume 1 and what one has to do in Volume 3 for the general case. In fact, when writing this text I have changed some of the original items, so that even more the description in the introduction of the first volume does not correctly describe the present procedure. Let me say a few words about the sources for the proofs of this volume and the citation policy. The breakthrough paper [B-W88] gave the general procedure and provided many ideas for the solution of the absolute toral rank 2 case. In the present exposition I stressed the point of using sandwich elements and graded algebras in combination with the BlockWeisfeiler description of these. The major contribution of sandwich element methods is due to A. A. P REMET . Most of the other material can be found in the papers [P-S 97][P-S 01]. I will not quote these results in detail. If the reader is interested in the original sources he should look into [B-W88], [Pre 85][Pre 94] and [P-S 97][P-S 01].
, the first chapter of this volume, is somewhat different from the rest. In that chapter we determine which of the Cartan type and Melikian algebras have absolute toral rank 2, determine automorphism groups of these algebras, describe orbits of toral elements in the minimal p -envelope under the automorphism group, compute the centralizers of toral elements and estimate the number of weights on restricted modules. In doing this we decover a lot of details of the structure of these algebras. This already indicates a weakness of the theory: at present one needs really much information on the algebra structures to apply some sophisticated arguments.
The notations in this volume and all references to Chapter 19 refer to the first volume. As a general assumption, F always denotes an algebraically closed field of characteristic p > 3 (while in the first volume we also included the case p = 3), and all algebras are regarded to be algebras over F .
Chapter 10
Tori in Hamiltonian and Melikian algebras
In this chapter we determine the Hamiltonian and Melikian algebras having absolute toral rank not bigger than 2. For those algebras the automorphism groups are determined and conjugacy classes of tori in the minimal p -envelopes are described. We gain structural insight in root spaces and sections with respect to 2-dimensional tori.
















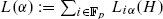 with respect to a toral CSA H , described their representations in the spaces
with respect to a toral CSA H , described their representations in the spaces 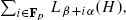 and determined 2-sections. The breakthrough paper [B-W88] made this procedure work for modular Lie algebras as well (if the characteristic is bigger than 7). It turned out, however, that the many more examples and the richness of their structures made things much more involved. Imagine that in the classical case only
and determined 2-sections. The breakthrough paper [B-W88] made this procedure work for modular Lie algebras as well (if the characteristic is bigger than 7). It turned out, however, that the many more examples and the richness of their structures made things much more involved. Imagine that in the classical case only 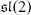 H ker occurs as the 1-section L (), while in the modular case the classical algebra
H ker occurs as the 1-section L (), while in the modular case the classical algebra  (1,1).
(1,1).