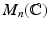1. Matrix Lie Groups
A previous version of this book was inadvertently published without the middle initial of the authors name as Brian Hall. For this reason an erratum has been published, correcting the mistake in the previous version and showing the correct name as Brian C. Hall (see DOI ). The version readers currently see is the corrected version. The Publisher would like to apologize for the earlier mistake.
1.1 Definitions
A Lie group is, roughly speaking, a continuous group , that is, a group described by several real parameters. In this book, we consider matrix Lie groups, which are Lie groups realized as groups of matrices. As an example, consider the set of all 2 2 real matrices with determinant 1, customarily denoted

. Since the determinant of a product is the product of the determinants, this set forms a group under the operation of matrix multiplication. If we think of the set of all 2 2 matrices, with entries a , b , c , d , as
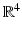
, then
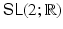
is the set of points in
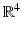
for which the smooth function
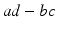
has the value 1.
Suppose f is a smooth function on
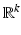
and we consider the set E where f ( x ) equals some constant value c . If, at each point x 0 in E , at least one of the partial derivatives of f is nonzero, then the implicit function theorem tells us that we can solve the equation f ( x )= c near x 0 for one of the variables as a function of the other k 1 variables. Thus, E is a smooth surface (or embedded submanifold ) in
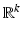
of dimension k 1. In the case of
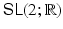
inside
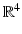
, we note that the partial derivatives of ad bc with respect to a , b , c , and d are d , c , b , and a , respectively. Thus, at each point where
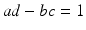
, at least one of these partial derivatives is nonzero, and we conclude that
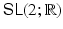
is a smooth surface of dimension 3. Thus,
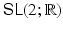
is a Lie group of dimension 3.
For other groups of matrices (such as the ones we will encounter later in this section), one could use a similar approach. The analysis is, however, more complicated because most of the groups are defined by setting several different smooth functions equal to constants. One therefore has to check that these functions are independent in the sense of the implicit function theorem, which means that their gradient vectors have to be linearly independent at each point in the group.
We will use an alternative approach that makes all such analysis unnecessary. We consider groups G of matrices that are closed in the sense of Definition ) will then show that G is a smooth manifold whose dimension is equal the dimension of
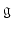
as a vector space.
This chapter makes use of various standard results from linear algebra, which are summarized in Appendix A.
Definition 1.1.
The general linear group over the real numbers, denoted
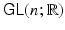
, is the group of all n n invertible matrices with real entries. The general linear group over the complex numbers, denoted
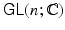
, is the group of all n n invertible matrices with complex entries.
Definition 1.2.
Let
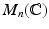
denote the space of all n n matrices with complex entries.
We may identify
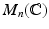
with
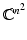
and use the standard notion of convergence in
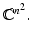
Explicitly, this means the following.
Definition 1.3.
Let A m be a sequence of complex matrices in
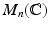
. We say that A m converges to a matrix A if each entry of A m converges (as m ) to the corresponding entry of A (i.e., if
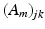
converges to A jk for all 1 j , k n ).
We now consider subgroups of
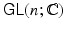
, that is, subsets G of
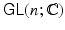
such that the identity matrix is in G and such that for all
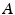
and B in G , the matrices AB and A 1 are also in G .
Definition 1.4.
A matrix Lie group is a subgroup G of
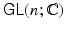
with the following property: If A m is any sequence of matrices in G , and A m converges to some matrix A , then either A is in G or A is not invertible.
The condition on G amounts to saying that G is a closed subset of
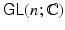
. (This does not necessarily mean that G is closed in
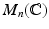
.) Thus, Definition is equivalent to saying that a matrix Lie group is a closed subgroup of
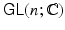
.
The condition that G be a closed subgroup, as opposed to merely a subgroup, should be regarded as a technicality, in that most of the interesting subgroups of
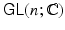
have this property. Most of the matrix Lie groups G we will consider have the stronger property that if A m is any sequence of matrices in G , and A m converges to some matrix A , then A G (i.e., that G is closed in
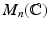














 . Since the determinant of a product is the product of the determinants, this set forms a group under the operation of matrix multiplication. If we think of the set of all 2 2 matrices, with entries a , b , c , d , as
. Since the determinant of a product is the product of the determinants, this set forms a group under the operation of matrix multiplication. If we think of the set of all 2 2 matrices, with entries a , b , c , d , as 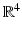 , then
, then 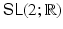 is the set of points in
is the set of points in 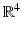 for which the smooth function
for which the smooth function 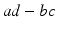 has the value 1.
has the value 1.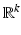 and we consider the set E where f ( x ) equals some constant value c . If, at each point x 0 in E , at least one of the partial derivatives of f is nonzero, then the implicit function theorem tells us that we can solve the equation f ( x )= c near x 0 for one of the variables as a function of the other k 1 variables. Thus, E is a smooth surface (or embedded submanifold ) in
and we consider the set E where f ( x ) equals some constant value c . If, at each point x 0 in E , at least one of the partial derivatives of f is nonzero, then the implicit function theorem tells us that we can solve the equation f ( x )= c near x 0 for one of the variables as a function of the other k 1 variables. Thus, E is a smooth surface (or embedded submanifold ) in 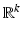 of dimension k 1. In the case of
of dimension k 1. In the case of 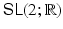 inside
inside 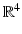 , we note that the partial derivatives of ad bc with respect to a , b , c , and d are d , c , b , and a , respectively. Thus, at each point where
, we note that the partial derivatives of ad bc with respect to a , b , c , and d are d , c , b , and a , respectively. Thus, at each point where 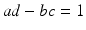 , at least one of these partial derivatives is nonzero, and we conclude that
, at least one of these partial derivatives is nonzero, and we conclude that 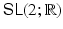 is a smooth surface of dimension 3. Thus,
is a smooth surface of dimension 3. Thus, 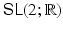 is a Lie group of dimension 3.
is a Lie group of dimension 3.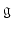 as a vector space.
as a vector space.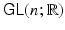 , is the group of all n n invertible matrices with real entries. The general linear group over the complex numbers, denoted
, is the group of all n n invertible matrices with real entries. The general linear group over the complex numbers, denoted 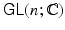 , is the group of all n n invertible matrices with complex entries.
, is the group of all n n invertible matrices with complex entries.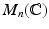 denote the space of all n n matrices with complex entries.
denote the space of all n n matrices with complex entries.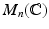 with
with 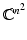 and use the standard notion of convergence in
and use the standard notion of convergence in 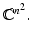 Explicitly, this means the following.
Explicitly, this means the following.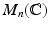 . We say that A m converges to a matrix A if each entry of A m converges (as m ) to the corresponding entry of A (i.e., if
. We say that A m converges to a matrix A if each entry of A m converges (as m ) to the corresponding entry of A (i.e., if 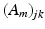 converges to A jk for all 1 j , k n ).
converges to A jk for all 1 j , k n ).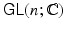 , that is, subsets G of
, that is, subsets G of 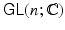 such that the identity matrix is in G and such that for all
such that the identity matrix is in G and such that for all 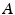 and B in G , the matrices AB and A 1 are also in G .
and B in G , the matrices AB and A 1 are also in G .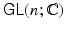 with the following property: If A m is any sequence of matrices in G , and A m converges to some matrix A , then either A is in G or A is not invertible.
with the following property: If A m is any sequence of matrices in G , and A m converges to some matrix A , then either A is in G or A is not invertible.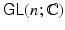 . (This does not necessarily mean that G is closed in
. (This does not necessarily mean that G is closed in 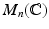 .) Thus, Definition is equivalent to saying that a matrix Lie group is a closed subgroup of
.) Thus, Definition is equivalent to saying that a matrix Lie group is a closed subgroup of 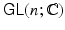 .
.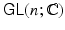 have this property. Most of the matrix Lie groups G we will consider have the stronger property that if A m is any sequence of matrices in G , and A m converges to some matrix A , then A G (i.e., that G is closed in
have this property. Most of the matrix Lie groups G we will consider have the stronger property that if A m is any sequence of matrices in G , and A m converges to some matrix A , then A G (i.e., that G is closed in