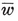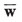Acknowledgments
Our greatest debt is to Sir Ronald A. Fisher, Jerzy Neyman, Egon S. Pearson, John von Neumann, and Abraham Wald. The present state of statistical theory is largely the result of their contributions which permeate this book. Particularly great is our debt to the late Abraham Wald who formulated statistics as decision making under uncertainty.
We acknowledge with warm thanks the keen and constructive comments of William H. Kruskal; we have acted upon many of his suggestions and have improved the book thereby. We thank Patrick Suppes for helpful comments on certain problems of mathematical notation. Harvey Wagner suggested that we incorporate the outline of a proof of the existence of the utility function as a handy reference for the mathematically sophisticated reader. He also proposed a proof which we found useful. Max Woods was especially effective in his careful preparation of the answers to the exercises and his detailed reading of the manuscript and proofs. Others who helped in reading the manuscript and proofs were Arthur Albert, Stuart Bessler, Judith Chernoff, Mary L. Epling, Joseph Kullback, Gerald Lenthall, Edward B. Perrin, Edythalena Tompkins, and Donald M. Ylvisaker. The completion of this manuscript would have long been delayed except for the unstinting cooperation of Carolyn Young, Charlotte Austin, Sharon Steck, and Max Woods. We thank our wives Judith Chernoff and Jean Moses for their support and encouragement.
The authors wish to express their appreciation to E. S. Pearson, C. Clopper, P. C. Mahalanobis, F. E. Croxton, and C. M. Thompson for the use of their tables. We are indebted to Professor Sir Ronald A. Fisher, Cambridge, to Dr. Frank Yates, Rothamsted, and to Messrs. Oliver and Boyd Ltd., Edinburgh, for permission to reprint Tables III, IV, and XXXIII from their book, Statistical Tables for Biological, Agricultural, and Medical Research.
H. C.
L. E. M.
APPENDIX A
Notation
RANDOM VARIABLES AND STATISTICS
A number which depends on the outcome of an experiment is a random variable. If we can compute it from observable data, it is called a statistic. All random variables and statistics are always indicated by boldfaced symbols. Since boldfaced symbols cannot easily be written we recommend for use on paper or at the blackboard that they be replaced by a corresponding symbol with an extra line through it. For example, we can use 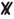 ,
,  , $ ,
, $ , 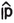 for X , Y , s ,
for X , Y , s , 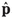 . We usually use capital roman letters for such symbols but there are occasional exceptions.
. We usually use capital roman letters for such symbols but there are occasional exceptions.
PARAMETERS
A property of the relevant probability distributions or of the state of nature is called a parameter. Parameters are usually denoted by Greek symbols. For example, we use , , , . An occasional exception such as p is made for the sake of tradition.
MODIFYING SYMBOLS
A dagger () next to a section indicates that this section is to be included in the course at the instructors option.
An asterisk (*) next to an exercise indicates that this exercise is important and should definitely be assigned to the class.
A circle () next to an exercise indicates that a solution of the exercise may require mathematical knowledge beyond the material usually covered in two years of high school mathematics.
A bar above a letter usually stands for the sample mean such as 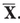 . We sometimes use it as an abbreviation for a point such as
. We sometimes use it as an abbreviation for a point such as 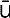 = ( x , y , z ).
= ( x , y , z ).
A breve above a letter stands for the sample median such as  .
.
A circumflex is used for an estimate, usually for a maximum-likelihood estimate, e.g., 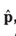 ,
, 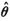 .
.
A tilde is used to denote the complement of a set. Thus 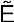 is the set of elements not in E.
is the set of elements not in E.
The symbols following a vertical bar represent an assumed condition or state of nature. For example, P { A | B } is the conditional probability of A given B, and f ( z |) represents the probability density function of Z when is the state of nature.
GLOSSARY OF LETTERS
The following is a highly detailed list of almost every letter which occurs with a special symbolic significance in this text. In studying the text, this glossary should not be often necessary. Few of these letters occur frequently. In no section of the book do many distinct symbols occur simultaneously. In context, the meaning of the symbols should ordinarily be clear. However, students who use this book for reference or for a brief review may find the following list occasionally helpful.
Lower Case Letters
| a | action |
| d | sample standard deviation |
| d | sample variance |
| f | probability density function, f ( x ), f ( z |) |
| f | observed frequency |
| l | loss function, l (, a ) |
| m | slope |
| m | binomial random variable (e.g., numbers of heads in n tosses of a coin) |
| n | sample size |
| p | probability |
| observed proportion |
| r | regret, r (, a ) |
| s | strategy, s ( Z ) |
| s | sample standard deviation |
| s | sample variance |
| t | estimator |
| t n | the t distribution with n degrees of freedom |
| u | utility function, u ( P ) |
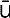 | point |
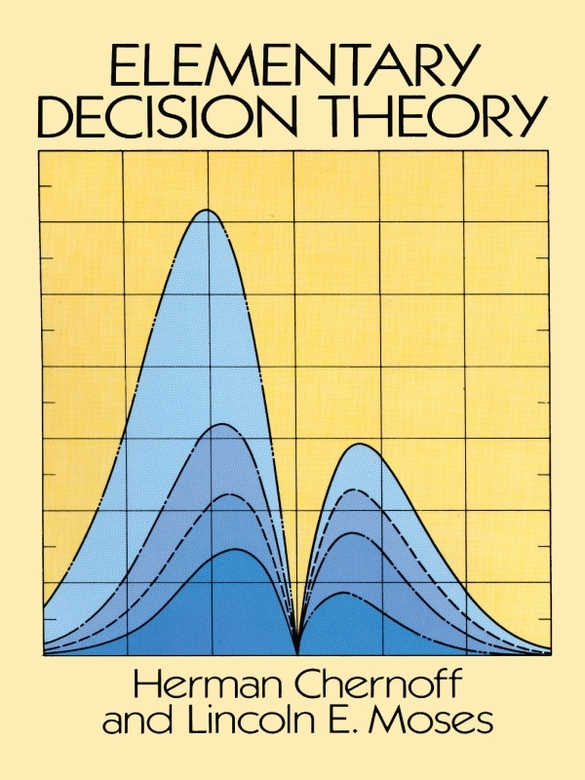
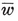 | set of weights or of a priori probabilities |
 | set of a posteriori probabilities |
| x | possible value of a random variable X |
| z | possible value for the entire collection of data Z |
Capital Letters
| A | acceptance set for H 1 |
| A | action taken, A = s ( Z ) |
| B | risk corresponding to the a priori probability ; B ( w , a ) |
| E | set or expectation ( E represents expectation when is the state of nature) |
| F | cumulative probability distribution function ( cdf ), F ( x ) |
| F | sample cumulative frequency function, F ( x ) |
| H | history or hypothesis |











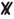 ,
,  , $ ,
, $ , 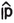 for X , Y , s ,
for X , Y , s , 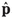 . We usually use capital roman letters for such symbols but there are occasional exceptions.
. We usually use capital roman letters for such symbols but there are occasional exceptions.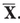 . We sometimes use it as an abbreviation for a point such as
. We sometimes use it as an abbreviation for a point such as 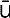 = ( x , y , z ).
= ( x , y , z ). .
.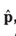 ,
, 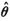 .
.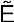 is the set of elements not in E.
is the set of elements not in E.