
WILEY SERIES IN PROBABILITY AND STATISTICS
ESTABLISHED BY WALTER A. SHEWHART AND SAMUEL S. WILKS
Editors: David J. Balding, Noel A. C. Cressie, Garrett M. Fitzmaurice, Geof H. Givens, Harvey Goldstein, Geert Molenberghs, David W. Scott, Adrian F. M. Smith, Ruey S. Tsay, Sanford Weisberg
Editors Emeriti: J. Stuart Hunter, Iain M. Johnstone, J. B. Kadane, Jozef L. Teugels
A complete list of the titles in this series appears at the end of this volume.
This edition first published 2014
2014 John Wiley & Sons, Ltd
Registered office
John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, United Kingdom
For details of our global editorial offices, for customer services and for information about how to apply for permission to reuse the copyright material in this book please see our website at www.wiley.com.
The right of the author to be identified as the author of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988.
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, except as permitted by the UK Copyright, Designs and Patents Act 1988, without the prior permission of the publisher.
Wiley also publishes its books in a variety of electronic formats. Some content that appears in print may not be available in electronic books.
Designations used by companies to distinguish their products are often claimed as trademarks. All brand names and product names used in this book are trade names, service marks, trademarks or registered trademarks of their respective owners. The publisher is not associated with any product or vendor mentioned in this book.
Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. It is sold on the understanding that the publisher is not engaged in rendering professional services and neither the publisher nor the author shall be liable for damages arising herefrom. If professional advice or other expert assistance is required, the services of a competent professional should be sought
Library of Congress Cataloging-in-Publication Data
Introduction to imprecise probabilities / edited by Thomas Augustin, Frank Coolen, Gert de Cooman,
Matthias Troffaes.
pages cm
Includes bibliographical references and index.
ISBN 978-0-470-97381-3 (hardback)
1. Probabilities. I. Augustin, Thomas, editor of compilation.
QA273.I56 2014
519.2 dc23
2013041146
A catalogue record for this book is available from the British Library.
ISBN: 978-0-470-97381-3
1 2014
Introduction
One of the big challenges for science is coping with uncertainty, omnipresent in modern societies and of ever increasing complexity. Quantitative modelling of uncertainty is traditionally based on the use of precise probabilities: for each event 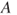 , a single (classical, precise) probability
, a single (classical, precise) probability 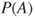 is assigned, typically implicitly assumed to satisfy Kolmogorov's axioms. Although there have been many successful applications of this concept, an increasing number of researchers in different areas keep warning that the concept of classical probability has severe limitations. The mathematical formalism of classical probability indispensably requires, and implicitly presupposes, an often unrealistically high level of precision and internal consistency of the information modelled, and thus relying on classical probability under complex uncertainty may lead to unjustified, and possibly deceptive, conclusions.
is assigned, typically implicitly assumed to satisfy Kolmogorov's axioms. Although there have been many successful applications of this concept, an increasing number of researchers in different areas keep warning that the concept of classical probability has severe limitations. The mathematical formalism of classical probability indispensably requires, and implicitly presupposes, an often unrealistically high level of precision and internal consistency of the information modelled, and thus relying on classical probability under complex uncertainty may lead to unjustified, and possibly deceptive, conclusions.
Against this background, a novel, more flexible theory of uncertainty has evolved: imprecise probabilities. Imprecise probabilities have proven a powerful and elegant framework for quantifying, as well as making inferences and decisions, under uncertainty. They encompass and extend the traditional concepts and methods of probability and statistics by allowing for incompleteness, imprecision and indecision, and provide new modelling opportunities where reliability of conclusions from incomplete information is important.
Given that it is a more flexible, and indeed a more honest description of complex uncertainty, the term imprecise probabilities taken literally is an unfortunate misnomer, which, regrettably, has provoked misunderstandings. Nevertheless imprecise probabilities has established itself as an umbrella term for related theories of generalized uncertainty quantification, most notably including lower and upper probabilities and lower and upper previsions. There a classical (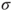 -) additive probability or a classical, linear prevision (expectation)
-) additive probability or a classical, linear prevision (expectation) 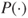 is replaced by an interval-valued set-function or functional
is replaced by an interval-valued set-function or functional 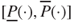 . For every gamble (random variable)
. For every gamble (random variable) 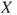 , the lower prevision
, the lower prevision 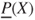 and the upper prevision
and the upper prevision 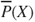 have a clear behavioural meaning as (typically different) supremum acceptable buying price and infimum acceptable selling price for
have a clear behavioural meaning as (typically different) supremum acceptable buying price and infimum acceptable selling price for 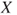 , respectively. For events
, respectively. For events 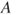 , the lower probability
, the lower probability 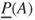 can informally be interpreted as reflecting the evidence certainly in favour of event
can informally be interpreted as reflecting the evidence certainly in favour of event 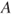 , while the upperprobability
, while the upperprobability 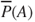 reflects all evidence possibly in favour of
reflects all evidence possibly in favour of 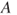 . Imprecise probabilities live in the continuum between two extreme cases: the case of classical probabilities and linear previsions where
. Imprecise probabilities live in the continuum between two extreme cases: the case of classical probabilities and linear previsions where 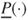 and
and 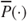 coincide, appropriate only if there is complete information on the stochastic behaviour of a perfect precise random process, and on the other extreme, the case of complete probabilistic ignorance, expressed by
coincide, appropriate only if there is complete information on the stochastic behaviour of a perfect precise random process, and on the other extreme, the case of complete probabilistic ignorance, expressed by 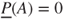 and
and 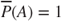 for all non-trivial events
for all non-trivial events 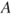 .
.
Using imprecise probabilities or related concepts seems very natural, and indeed it has a long tradition (see, in particular, [343] for a review). The first formal treatment dates back at least to Boole's book [81] in the middle of the nineteenth century. Further milestones include among others the work of Keynes [394] on incomplete probability orderings; Smith's [602] introduction of lower and upper betting odds and Williams' [702] generalization of coherence; Ellsberg's [264] experiments demonstrating the constitutive role of complex uncertainty in rational decision making; Dempster's [222] concept of multivalued mappings in inference, and its powerful reinterpretation by Shafer [576], that became particularly popular in artificial intelligence (Dempster-Shafer theory of belief functions); Huber's [367] reflection on the power of capacity-based neighbourhoods models in robust statistics; and Walley and Fine's [678] work on a frequentist theory of lower and upper probabilities.
Next page










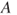 , a single (classical, precise) probability
, a single (classical, precise) probability 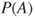 is assigned, typically implicitly assumed to satisfy Kolmogorov's axioms. Although there have been many successful applications of this concept, an increasing number of researchers in different areas keep warning that the concept of classical probability has severe limitations. The mathematical formalism of classical probability indispensably requires, and implicitly presupposes, an often unrealistically high level of precision and internal consistency of the information modelled, and thus relying on classical probability under complex uncertainty may lead to unjustified, and possibly deceptive, conclusions.
is assigned, typically implicitly assumed to satisfy Kolmogorov's axioms. Although there have been many successful applications of this concept, an increasing number of researchers in different areas keep warning that the concept of classical probability has severe limitations. The mathematical formalism of classical probability indispensably requires, and implicitly presupposes, an often unrealistically high level of precision and internal consistency of the information modelled, and thus relying on classical probability under complex uncertainty may lead to unjustified, and possibly deceptive, conclusions.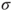 -) additive probability or a classical, linear prevision (expectation)
-) additive probability or a classical, linear prevision (expectation) 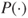 is replaced by an interval-valued set-function or functional
is replaced by an interval-valued set-function or functional 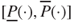 . For every gamble (random variable)
. For every gamble (random variable) 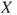 , the lower prevision
, the lower prevision 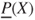 and the upper prevision
and the upper prevision 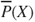 have a clear behavioural meaning as (typically different) supremum acceptable buying price and infimum acceptable selling price for
have a clear behavioural meaning as (typically different) supremum acceptable buying price and infimum acceptable selling price for 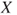 , respectively. For events
, respectively. For events 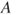 , the lower probability
, the lower probability 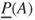 can informally be interpreted as reflecting the evidence certainly in favour of event
can informally be interpreted as reflecting the evidence certainly in favour of event 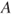 , while the upperprobability
, while the upperprobability 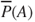 reflects all evidence possibly in favour of
reflects all evidence possibly in favour of 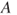 . Imprecise probabilities live in the continuum between two extreme cases: the case of classical probabilities and linear previsions where
. Imprecise probabilities live in the continuum between two extreme cases: the case of classical probabilities and linear previsions where 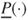 and
and 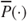 coincide, appropriate only if there is complete information on the stochastic behaviour of a perfect precise random process, and on the other extreme, the case of complete probabilistic ignorance, expressed by
coincide, appropriate only if there is complete information on the stochastic behaviour of a perfect precise random process, and on the other extreme, the case of complete probabilistic ignorance, expressed by 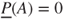 and
and 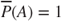 for all non-trivial events
for all non-trivial events 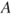 .
.