• Complain
LitArk » Books » Home and family

U. Narayan Bhat - An Introduction to Queueing Theory: Modeling and Analysis in Applications

Here you can read online U. Narayan Bhat - An Introduction to Queueing Theory: Modeling and Analysis in Applications full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2015, publisher: Birkhäuser, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:

Romance novel Science fiction Adventure Detective Science History Home and family Prose Art Politics Computer Non-fiction Religion Business Children Humor

Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.

U. Narayan Bhat An Introduction to Queueing Theory: Modeling and Analysis in Applications
  • Book:
    An Introduction to Queueing Theory: Modeling and Analysis in Applications
  • Author:
  • Publisher:
    Birkhäuser
  • Genre:
  • Year:
    2015
  • Rating:
    3 / 5
  • Favourites:
    Add to favourites
  • Your mark:
    • 60
    • 1
    • 2
    • 3
    • 4
    • 5

An Introduction to Queueing Theory: Modeling and Analysis in Applications: summary, description and annotation

We offer to read an annotation, description, summary or preface (depends on what the author of the book "An Introduction to Queueing Theory: Modeling and Analysis in Applications" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.

This introductory textbook is designed for a one-semester course on queueing theory that does not require a course on stochastic processes as a prerequisite. By integrating the necessary background on stochastic processes with the analysis of models, the work provides a sound foundational introduction to the modeling and analysis of queueing systems for a broad interdisciplinary audience of students in mathematics, statistics, and applied disciplines such as computer science, operations research, and engineering. This edition includes additional topics in methodology and applications.

Key features:

An introductory chapter including a historical account of the growth of queueing theory in more than 100 years.

A modeling-based approach with emphasis on identification of models

Rigorous treatment of the foundations of basic models commonly used in applications with appropriate references for advanced topics.

A chapter on matrix-analytic method as an alternative to the traditional methods of analysis of queueing systems.

A comprehensive treatment of statistical inference for queueing systems.

Modeling exercises and review exercises when appropriate.

The second edition of An Introduction of Queueing Theory may be used as a textbook by first-year graduate students in fields such as computer science, operations research, industrial and systems engineering, as well as related fields such as manufacturing and communications engineering. Upper-level undergraduate students in mathematics, statistics, and engineering may also use the book in an introductory course on queueing theory. With its rigorous coverage of basic material and extensive bibliography of the queueing literature, the work may also be useful to applied scientists and practitioners as a self-study reference for applications and further research.

...This book has brought a freshness and novelty as it deals mainly with modeling and analysis in applications as well as with statistical inference for queueing problems. With his 40 years of valuable experience in teaching and high level research in this subject area, Professor Bhat has been able to achieve what he aimed: to make [the work] somewhat different in content and approach from other books. - Assam Statistical Review of the first edition

U. Narayan Bhat: author's other books


Who wrote An Introduction to Queueing Theory: Modeling and Analysis in Applications? Find out the surname, the name of the author of the book and a list of all author's works by series.


U. Narayan Bhat - An Introduction to Queueing Theory: Modeling and Analysis in Applications
An Introduction to Queueing Theory: Modeling and Analysis in Applications
U. Narayan Bhat
An Introduction to Queueing Theory: Modeling and Analysis in Applications

An Introduction to Queueing Theory: Modeling and Analysis in Applications — read online for free the complete book (whole text) full work

Below is the text of the book, divided by pages. System saving the place of the last page read, allows you to conveniently read the book "An Introduction to Queueing Theory: Modeling and Analysis in Applications" online for free, without having to search again every time where you left off. Put a bookmark, and you can go to the page where you finished reading at any time.

Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make
1234567...166
Springer Science+Business Media New York 2015
U. Narayan Bhat An Introduction to Queueing Theory Statistics for Industry and Technology 10.1007/978-0-8176-8421-1_1
1. Introduction
U. Narayan Bhat 1
(1)
Department of Statistical Science, Southern Methodist University, Dallas, Texas, USA
1.1
1.2
1.3
1.4
1.1 Basic System Elements
Queues (or waiting lines) help facilities or businesses provide service in an orderly fashion. Forming a queue being a social phenomenon, it is beneficial to the society if it can be managed so that both the unit that waits and the one that serves get the most benefit. For instance, there was a time when in airline terminals passengers formed separate queues in front of check-in counters. But now we see invariably only one line feeding into several counters. This is the result of the realization that a single line policy serves better for the passengers as well as the airline management. Such a conclusion has come from analyzing the mode by which a queue is formed and the service is provided. The analysis is based on building a mathematical model representing the process of arrival of passengers who join the queue, the rules by which they are allowed into service, and the time it takes to serve the passengers. Queueing theory embodies the full gamut of such models covering all perceivable systems which incorporate characteristics of a queue.
We identify the unit demanding service, whether it is human or otherwise, as customer . The unit providing service is known as the server . This terminology of customers and servers is used in a generic sense regardless of the nature of the physical context. Some examples are given below:
(a)
In communication systems, voice or data traffic queue up for lines for transmission. A simple example is the telephone exchange.
(b)
In a manufacturing system with several work stations, units completing work in one station wait for access to the next.
(c)
Vehicles requiring service wait for their turn in a garage.
(d)
Patients arrive at a doctors clinic for treatment.
Numerous examples of this type are of everyday occurrence. While analyzing them we can identify some basic elements of the systems.
Input Process
If the occurrence of arrivals and the offer of service are strictly according to schedule, a queue can be avoided. But in practice this does not happen. In most cases, the arrivals are the product of external factors. Therefore, the best one can do is to describe the input process in terms of random variables that represent either the number arriving during a time interval or the time interval between successive arrivals. If customers arrive in groups, their size can be a random variable as well.
Service Mechanism
The uncertainties involved in the service mechanism are the number of servers, the number of customers getting served at any time, and the duration and mode of service. Networks of queues consist of more than one server arranged in series and/or parallel. Random variables are used to represent service times, and the number of servers, when appropriate. If service is provided for customers in groups, their size can also be a random variable.
System Capacity
The number of customers that can wait at a time in a queueing system is a significant factor for consideration. If the waiting room is large, one can assume that for all practical purposes, it is infinite. But our everyday experience with the telephone systems tells us that the size of the buffer that accommodates our call while waiting to get a free line is important as well.
Queue Discipline
All other factors regarding the rules of conduct of the queue can be pooled under this heading. One of these is the rule followed by the server in accepting customers for service. In this context, the rules such as first-come, first-served (FCFS), last-come, first-served (LCFS), and random selection for service (RS) are self-explanatory. Others such as round robin and shortest processing time may need some elaboration, which is provided in later chapters. In many situations, customers in some classes get priority for service over others. There are many other queue disciplines which have been introduced for the efficient operation of computers and communication systems. Also, there are other factors of customer behavior such as balking, reneging, and jockeying, that require consideration as well.
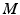The identification of these elements provides a taxonomy for symbolically representing queueing systems with a variety of system elements. The basic representation widely used in queueing theory is due to D. G. Kendall (1953) and made up of symbols representing three elements: input, service, and number of servers. 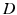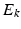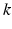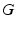For instance, using Picture 1 for Poisson or exponential, Picture 2 for deterministic (constant), Picture 3 for the Erlang distribution with scale parameter Picture 4 , and Picture 5 for general (also 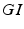Picture 6 , for general independent) we write:
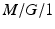Picture 7 : Poisson arrivals, general service, single server
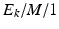Picture 8 : Erlangian arrival, exponential service, single server
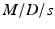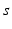Picture 9 : Poisson arrival, constant service, Picture 10 servers.
These symbolic representations are modified when other factors are involved.
1.2 Problems in a Queueing System
The ultimate objective of the analysis of queueing systems is to understand the behavior of their underlying processes so that informed and intelligent decisions can be made in their management. Three types of problems can be identified in this process.
Behavioral Problems
The study of behavioral problems of queueing systems is intended to understand how they behave under various conditions. The bulk of the results in queueing theory is based on research on behavioral problems. Mathematical models for the probability relationships among the various elements of the underlying process are used in the analysis. To make the ideas concrete let us define a few terms that are defined formally later. A collection or a sequence of random variables that are indexed by a parameter such as time is known as a stochastic process ; e.g., an hourly record of the number of accidents occurring in a city. In the context of a queueing system, the number of customers with time as the parameter is a stochastic process. 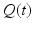Let Picture 11 be the number of customers in the system at time 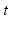Picture 12 . This number is the difference between the number of arrivals and departures during Picture 13
Next page
1234567...166
Light

Font size:

↓
↑
Reset

Interval:

↓
↑

Bookmark:

Make

Similar books «An Introduction to Queueing Theory: Modeling and Analysis in Applications»

Look at similar books to An Introduction to Queueing Theory: Modeling and Analysis in Applications. We have selected literature similar in name and meaning in the hope of providing readers with more options to find new, interesting, not yet read works.


Christos G. Cassandras - Introduction to Discrete Event Systems
Introduction to Discrete Event Systems
Christos G. Cassandras
Introduction to Discrete Event Systems
Albert N. Shiryaev (editor) - Recent Developments in Stochastic Methods and Applications: ICSM-5, Moscow, Russia, November 23–27, 2020, Selected Contributions: 371 (Springer Proceedings in Mathematics & Statistics, 371)
Recent Developments in Stochastic Methods and Applications: ICSM-5, Moscow, Russia, November 23–27, 2020, Selected Contributions: 371 (Springer Proceedings in Mathematics & Statistics, 371)
Albert N. Shiryaev (editor)
Recent Developments in Stochastic Methods and Applications: ICSM-5, Moscow, Russia, November 23–27, 2020, Selected Contributions: 371 (Springer Proceedings in Mathematics & Statistics, 371)
Rafajłowicz Ewaryst - Stochastic Models, Statistics and Their Applications: Wrocław, Poland, February 2015
Stochastic Models, Statistics and Their Applications: Wrocław, Poland, February 2015
Rafajłowicz Ewaryst
Stochastic Models, Statistics and Their Applications: Wrocław, Poland, February 2015
No cover
No cover
Ross
Introduction to Probability Models
No cover
No cover
Yang
Engineering Mathematics with Examples and Applications
Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c
Queues and Lévy Fluctuation Theory [recurso electrónico] $c
Dębicki Krzysztof
Queues and Lévy Fluctuation Theory [recurso electrónico] $c
Gerard-Michel Cochard - Introduction to stochastic processes and simulation
Introduction to stochastic processes and simulation
Gerard-Michel Cochard
Introduction to stochastic processes and simulation
Nicolas Lanchier - Stochastic Modeling
Stochastic Modeling
Nicolas Lanchier
Stochastic Modeling
Narsingh Deo - Graph Theory with Applications to Engineering and Computer Science
Graph Theory with Applications to Engineering and Computer Science
Narsingh Deo
Graph Theory with Applications to Engineering and Computer Science
Pierre Brémaud - Fourier Analysis and Stochastic Processes
Fourier Analysis and Stochastic Processes
Pierre Brémaud
Fourier Analysis and Stochastic Processes
No cover
No cover
Barry L. Nelson
Stochastic Modeling: Analysis and Simulation
No cover
No cover
Donald Gross
Fundamentals of Queueing Theory
Reviews about «An Introduction to Queueing Theory: Modeling and Analysis in Applications»

Discussion, reviews of the book An Introduction to Queueing Theory: Modeling and Analysis in Applications and just readers' own opinions. Leave your comments, write what you think about the work, its meaning or the main characters. Specify what exactly you liked and what you didn't like, and why you think so.