Part 1
Basic Mathematical Concepts
Basic Reminders of Probability
CONCEPTS DISCUSSED IN THIS CHAPTER. The concept of probability is at the heart of this book. It is therefore necessary to master the corresponding concepts. In principle, the reader should already have the required knowledge. However, experience shows that a reminder is always necessary to refresh knowledge which may have been learnt a while ago.
In this chapter, we will discuss the nature of chance and an empirical approach to probability, based on counting possible results from experience.
We will move on to a formal approach to probability, based on the set theory, which applies to previous experimental cases, and then a statistical definition of probability with the law of large numbers.
If the reader is proficient in these concepts, they can skip the corresponding sections.
Finally, we will end with the very important concept of composite probability, which is illustrated by a figure showing states of a system, transitions between states and graphs representative of the possible evolution of a system.
Recommended reading: [BRE 09, DEH 82, DOD 08, ENG 76, ROS 93, SAP 11].
1.1. Chance
The Larousse dictionary gives two meanings for the word chance:
- power regarded as the cause of apparently incidental or inexplicable events;
- unforeseen or unforeseeable circumstances, the effects of which may be favorable or unfavorable to someone.
The first definition is actually a double one:
- it introduces the concept of causality according to which an inexplicable event would nevertheless be due to an unknown cause; knowing the cause and the mechanisms that result from it, one could (theoretically) explain the inexplicable. Thus, if a passerby is hit on the head by a flowerpot that has fallen from a window after a gust of wind, it is tempting to say that this event is incidental; however, it is quite explainable. If an observer looks at the situation, he or she can indeed see that the accident is inevitable. One could even, if the problem was not so complex, explain the accident with the laws of mechanics. Inexplicable does not mean chance;
- it also suggests that the cause is a power. God, maybe? Let us quote the famous answer given by Pierre-Simon de Laplace to Napoleon when asked why he did not mention the existence of God in his Treatise of celestial mechanics: Sire, I had no need of that hypothesis.
The second definition brings us to the fundamental subject of this book: can hazardous events be predicted? This question will lead to probability theory. It originates from games called games of chance. Chevalier de Meres bet is representative of the reflections of the time when the theory of probability was born, with Blaise Pascal and Pierre de Fermat. According to Chevalier de Mere, who had noted that as throwing a die four times had a good chance of getting a 6, it should be even more rewarding to get a double 6 by rolling 24 dice twice. Pascal showed him that his reasoning was wrong. In the first case, the probability of rolling a 6 is 0.517, while in the second case, the probability of rolling a double 6 is only 0.4911. Here, we are already calculating probability, which indicates the concept of forecasting: it does not give the definite result, but the chances of obtaining a given result.
1.2. Counting and probability
It is common when first looking at probability to take widely used examples, namely rolling a six-sided die numbered from 1 to 6, or picking out colored balls from a bag containing a certain number of balls that differ only in color, or taking cards from a deck of cards. It is very rare that a presentation on the concept of probability does not use these three examples. We will follow this custom and use these three easy-to-imagine examples, but later we will look at other examples more related to everyday life (we do not generally spend all our time playing dice, choosing balls from a bag or playing cards!).

Figure 1.1. Pierre de Fermat (16011665) and Blaise Pascal (16231662) can be considered the founding fathers of the mathematical branch we call probability calculation today. These men exchanged letters during their research, posing problems to solve, but never met
EXAMPLE 1.1. First, roll the die and consider our chances of getting a 5. Assuming it is a fair die (we have as many chances to get any result with such a die), we can already say that our chances of getting a 5 are the same as those of getting a 1, 2, 3, 4 or 6. This is expressed by saying that the various results are equiprobable.
As we have six possible results and only one effective result, we can say that, to get a given result, we have 1 chance in 6, which we can express by the ratio 1/6, representing the probability of having one of the possible outcomes. This ratio expresses the quotient of the number of favorable results (here 1) to the number of possible outcomes (here 6). We can then use an abbreviated notation p(result = a) = 1/6 where a is an integer between 1 and 6. The sum of all the probabilities is 6 (1/6), so 1.
In addition, suppose that we are interested in result a. Every result that is not this one (not a) is a contrary result.
As a result, p(result = a) + p(result = not a) = 1, the sum of the probability of a result and the probability of the opposite result is equal to 1.
EXAMPLE 1.2(1). Now let us look at the bag containing identical black and white balls. Imagine we have three black balls and two white balls. If we pick out a ball, (without looking, of course) what are our chances of getting a black ball?
This problem is less simple that the previous one. However, we can say that we have more chances to get a black ball than to get a white ball because there are more black balls than white balls. If we try to identify the balls in the bag using thought, we can see that there can be five possible results, of which three correspond to our expectation (picking out a black ball).
This situation is expressed by the ratio 3/5 and p(picking out a black ball) = 3/5.
Similarly, we can express the ratio 2/5, the chances of obtaining the draw of a white ball, as p(picking out a white ball) = 2/5. Here again, the probability is expressed as the ratio of the number of expected results (here 3 for the black balls and 2 for the white balls) to the number of possible results (here 5).
Note that, unlike the previous example, picking out a black ball and picking out a white ball are not equiprobable: 3/5 probability in one case, 2/5 probability in the other. Note also that the sum of the probabilities of the result of picking out a ball is 3/5 + 2/5 = 1.
EXAMPLE 1.3(1). Let us move on to the card deck. Imagine taking 2 cards from a deck of 52 cards (13 cards of each color) and trying to estimate the odds of drawing two aces.
Let us first estimate all the possible results by naming the two cards X and Y. For the first card drawn, X, there are 52 possibilities and there are 51 cards in the deck for the second card, Y. But the roles of X and Y are interchangeable, so that in all we have (52 51)/2 possibilities to not count the same result twice, i.e. 1,326 possible results. There are four aces in the deck, so we have four possibilities for the first ace X and more than three possibilities for the second ace Y; by exchanging the roles of X and Y, we have either (4 3)/2 = 6 expected results, which we can easily list:
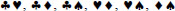






![Dębicki Krzysztof - Queues and Lévy Fluctuation Theory [recurso electrónico] $c](/uploads/posts/book/193156/thumbs/d-bicki-krzysztof-queues-and-l-vy-fluctuation.jpg)