Nicolas Lanchier - Stochastic Modeling
Here you can read online Nicolas Lanchier - Stochastic Modeling full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. year: 2017, publisher: Springer, genre: Children. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Stochastic Modeling
- Author:
- Publisher:Springer
- Genre:
- Year:2017
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Stochastic Modeling: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Stochastic Modeling" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Three coherent parts form the material covered in this text, portions of which have not been widely covered in traditional textbooks. In this coverage the reader is quickly introduced to several different topics enriched with 175 exercises which focus on real-world problems. Exercises range from the classics of probability theory to more exotic research-oriented problems based on numerical simulations. Intended for graduate students in mathematics and applied sciences, the text provides the tools and training needed to write and use programs for research purposes.
The first part of the text begins with a brief review of measure theory and revisits the main concepts of probability theory, from random variables to the standard limit theorems. The second part covers traditional material on stochastic processes, including martingales, discrete-time Markov chains, Poisson processes, and continuous-time Markov chains. The theory developed is illustrated by a variety of examples surrounding applications such as the gamblers ruin chain, branching processes, symmetric random walks, and queueing systems. The third, more research-oriented part of the text, discusses special stochastic processes of interest in physics, biology, and sociology. Additional emphasis is placed on minimal models that have been used historically to develop new mathematical techniques in the field of stochastic processes: the logistic growth process, the Wright Fisher model, Kingmans coalescent, percolation models, the contact process, and the voter model. Further treatment of the material explains how these special processes are connected to each other from a modeling perspective as well as their simulation capabilities in C and Matlab.Nicolas Lanchier: author's other books
Who wrote Stochastic Modeling? Find out the surname, the name of the author of the book and a list of all author's works by series.












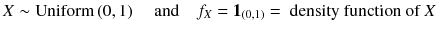
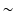 means that the law of the random variable on the left-hand side is given by the right-hand side. Then, the probability to be found is
means that the law of the random variable on the left-hand side is given by the right-hand side. Then, the probability to be found is 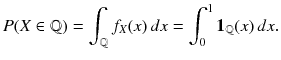
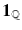 is known as the Dirichlet function. To find its integral, recall that the Riemann sum of a function is defined from a tagged partition of the domain of the function as illustrated on the left-hand side of Figure ) does not exist. Using the framework of measure theory, however, we can properly define and compute this integral. This is done at the end of the next section.
is known as the Dirichlet function. To find its integral, recall that the Riemann sum of a function is defined from a tagged partition of the domain of the function as illustrated on the left-hand side of Figure ) does not exist. Using the framework of measure theory, however, we can properly define and compute this integral. This is done at the end of the next section. 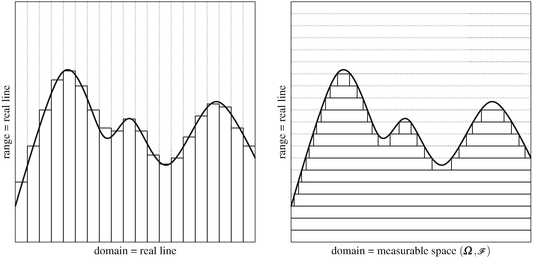
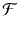 of subsets of is said to be a -algebra whenever
of subsets of is said to be a -algebra whenever 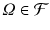
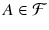 , we have
, we have 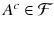
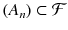 , we have
, we have 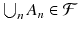 .
.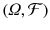 is then called a measurable space .
is then called a measurable space .