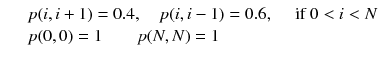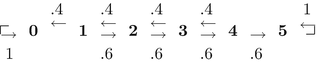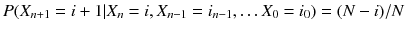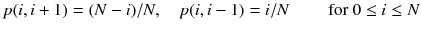Durrett - Essentials of Stochastic Processes
Here you can read online Durrett - Essentials of Stochastic Processes full text of the book (entire story) in english for free. Download pdf and epub, get meaning, cover and reviews about this ebook. City: Cham, year: 2016;2018, publisher: Springer International Publishing, genre: Home and family. Description of the work, (preface) as well as reviews are available. Best literature library LitArk.com created for fans of good reading and offers a wide selection of genres:
Romance novel
Science fiction
Adventure
Detective
Science
History
Home and family
Prose
Art
Politics
Computer
Non-fiction
Religion
Business
Children
Humor
Choose a favorite category and find really read worthwhile books. Enjoy immersion in the world of imagination, feel the emotions of the characters or learn something new for yourself, make an fascinating discovery.
- Book:Essentials of Stochastic Processes
- Author:
- Publisher:Springer International Publishing
- Genre:
- Year:2016;2018
- City:Cham
- Rating:3 / 5
- Favourites:Add to favourites
- Your mark:
Essentials of Stochastic Processes: summary, description and annotation
We offer to read an annotation, description, summary or preface (depends on what the author of the book "Essentials of Stochastic Processes" wrote himself). If you haven't found the necessary information about the book — write in the comments, we will try to find it.
Building upon the previous editions, this textbook is a first course in stochastic processes taken by undergraduate and graduate students (MS and PhD students from math, statistics, economics, computer science, engineering, and finance departments) who have had a course in probability theory. It covers Markov chains in discrete and continuous time, Poisson processes, renewal processes, martingales, and option pricing. One can only learn a subject by seeing it in action, so there are a large number of examples and more than 300 carefully chosen exercises to deepen the readers understanding.
Drawing from teaching experience and student feedback, there are many new examples and problems with solutions that use TI-83 to eliminate the tedious details of solving linear equations by hand, and the collection of exercises is much improved, with many more biological examples. Originally included in previous editions, material too advanced for this first course in...
Durrett: author's other books
Who wrote Essentials of Stochastic Processes? Find out the surname, the name of the author of the book and a list of all author's works by series.